Ctrl+K

卷积神经网络推理 (3)：基于 L2 缓存优化的 Winograd 卷积的 C++ 实现

10. 卷积神经网络推理 (3)：基于 L2 缓存优化的 Winograd 卷积的 C++ 实现#

公开时间：2022-09-04

备注

该工作是第五届 Ubiquant Challenge 量化新星挑战赛|并行程序设计竞赛的初赛入围工作，有一定的补充和删减。该工作在【天之孔】队长强宜澄的牵头下完成。

这份文档是使用 Winograd 算法高效实现 \(3 \times 3\) 卷积核神经网络的推理过程，并会作补充讨论。程序与初赛提交版本不同，对于程序可读性与规范性作改进，但算法思路完全一致。

【天之孔】

  1. Fate/Grand Order (作为 Fate/EXTRA CCC 衍生作品) 瞑生院祈荒 宝具。在人从苦界解脱并落入天之孔时，瞑生院可以感受到至高的愉悦。

  2. 天坑。代指天坑专业，如本队队员所处的化学专业、高分子专业。

危险

初赛部分的程序与大部分文档是由我完成的，本篇文档也只介绍这部分初赛工作，且绝非是最高效实现。这些也都整理到 gitee: ajz34/winograd6x3 中。

文档作者并没有计算机或高性能计算的专业知识。不能保证文档内容正确性或术语严格。

在并行程序设计决赛中，我们小组 (第二名) 在 Winograd 题中所使用的代码，是由强哥完成 (紧抱大腿 ≥ω≤)。尽管实现的仍然是 Winograd \(F(6, 3)\)、图像与卷积核变换代码与初赛相同，但除此之外的算法逻辑与程序完全不同、且更为高效。核心的改进点应是在指令集级别，参考 openBlas 对 DGEMM 等函数的多级缓存优化、micro-kernel 优化、计算过程隐藏读写延迟，以及适应性更广的边界情形处理等等。

赛题 baseline 请参考 gitee: benjie-miao/winograd-baseline。决赛获得冠军队伍的工作，请参考 github: Robslhc/ubiquant-winograd。

在上一篇文档中，我们已经介绍了 Winograd 算法的具体过程与实现；但对 Winograd 算法的强大之处，之前只作定性上的讨论。

在这一篇文档，我们会讨论 Winograd 算法的实现，并且具体地表明 Winograd \(F(6,3)\) 算法相对于 Direct 算法的效率提升比例。我们可能会发现，合理地利用缓存 (cache) 和并行，对程序效率的提升是非常可观的；它甚至可能超过 Winograd 算法本身的效率提升。同时，我们也会尽可能利用 AVX 指令集，尽可能优化编译过程。最后我们程序的实现效率在大并行的情况下，在相当短的代码量下 (不使用汇编或大量宏代码共约 400 行)，VGG16 平均效率会高于 oneDNN 库函数实现。

尽管本文档并非是最高效率的实现，但我希望能借这样的机会，以非专业的角度，表述我在学习高性能计算问题时的一些步伐与心得。也希望能对同样非专业的同行们以一些启发。

警告

请注意，本文档使用 cling-xeus 引擎的 Jupyter Notebook。该引擎通常可以正确地编译并执行 C++ 代码，但无法在效率上与开足优化的 g++ 相比。因此，本文并不对 Jupyter Notebook 的 code block 进行耗时比较；而是使用 g++ 编译所得程序实现比较。

// NOTE: cling-xeus jupyter automatically includes common headers
//       such as vector, algorithms, chrono, ...
#include <iostream>
#include <chrono>
#include <immintrin.h>
#include <xmmintrin.h>

// use an appropriate omp path for your own 
#include "/share/Pub/zyzhu/miniconda3/lib/gcc/x86_64-conda-linux-gnu/9.3.0/include/omp.h"

// override default libgomp to avoid link failure in xcpp
#pragma cling load("libiomp5")

using namespace std;

omp_set_num_threads(8);

一些方便的函数定义如下：

  • allclose 函数用于验证两个向量的每个元素是否相等：

/// Check if vector a[s] and b[s] are close by checking every element
bool allclose(float * a, float * b, size_t s,
              float rtol=1e-4, float atol=1e-4) {
    for (size_t i = 0; i < s; ++i)
        if (abs(a[i] - b[i]) > (atol + rtol * abs(b[i]))) return false;
    return true;
}

  • ceildiv 函数用于给出天花板整数除：

template<typename T>
inline T ceildiv(T a, T b) {
    return (a + b - 1) / b;
}

  • product 函数给出数组的连乘积：

template<typename T>
inline T product(const std::vector<T>& v) {
    return std::accumulate(v.cbegin(), v.cend(), 1, std::multiplies<T>());
}

  • rand_vec 函数会生成随机数向量，随机数区间为 [0, 10)：

template<typename T>
void rand_vec(T* v, size_t n) {
    for (size_t i = 0; i < n; ++i)
        v[i] = (T(rand()) / T(RAND_MAX)) * 10;
}

  • Range 类用于储存迭代序号信息 (通过成员变量 start, end 给出迭代的起始、终点位置，成员函数 size 给出迭代次数)：

struct Range {
    int start;
    int end;
    Range(): start(-1), end(-1) {}
    Range(int start, int end): start(start), end(end) {}
    inline int size() const { return end - start; }
};

10.1. 示例问题：经过更改的 VGG16 conv(3.2)#

我们在该文档的大部分时候，都会使用下述 VGG16 conv(3.2) 卷积层作为演示示例。只有在文档最后的测评阶段，我们才会使用完整的 VGG16 网络 [1]。

  • 输入图像的高度 IH \(H_\mathrm{in} = 56\)，宽度 IW \(W_\mathrm{in} = 56\)；

  • 输入通道数 IC \(C_\mathrm{in} = 256\)，输出通道数 OC \(C_\mathrm{out} = 256\)；

  • 每批图像数量 N \(N = 8\)。

导出量是

  • 输出图像的高度 OH \(H_\mathrm{out} = 54\)，宽度 OW \(W_\mathrm{out} = 54\)。

  • Winograd 算法需要在高方向上处理 TH \(\tilde H = \lceil H_\mathrm{out} / 6 \rceil = 9\) 次，宽方向也是 TW \(\tilde W = 9\)。当前情形不需要考虑无法整除时的边界情况。

关键的输入、输出张量是

  • 输入图像 image \(d_{i,c,x,y}\)，维度 \((N, C_\mathrm{in}, H_\mathrm{in}, W_\mathrm{in})\)；

  • 卷积核 filtr \(g_{k,c,u,v}\)，维度 \((C_\mathrm{out}, C_\mathrm{in}, 3, 3)\)

  • 输出图像 result \(Y_{i,k,x,y}\)，维度 \((N, C_\mathrm{out}, H_\mathrm{out}, W_\mathrm{out})\)；

其中，输入图像与卷积核是输入量、输出图像是输出量。

size_t IH = 56, IW = 56, IC = 256, OC = 256, N = 8;
size_t OH = IH - 2, OW = IW - 2;
size_t TH = ceildiv<size_t>(OH, 6), TW = ceildiv<size_t>(OW, 6);

vector<size_t> dim_image  {  N, IC, IH, IW };
vector<size_t> dim_filtr  { OC, IC,  3,  3 };
vector<size_t> dim_result {  N, OC, OH, OW };

size_t size_image  = product<size_t>(dim_image);
size_t size_filtr  = product<size_t>(dim_filtr);
size_t size_result = product<size_t>(dim_result);

在 C++ 程序中，我们有意不使用便利的库 (譬如 Eigen)，也不使用 std::vector 储存矩阵或张量。我们简单地使用 float *。

  • 使用 float * 的好处是，它就是简单的指针；如果程序要开放以 C 语言为函数的接口，那么就省去了从 std::vector<float> 到 float * 的转换过程。

  • 在控制向量的对齐时，使用 float * 会非常方便。向量的对齐 (align) 通常在存读数据时有一定优势。

  • 但 float * 的明显缺点是，其使用不是很安全，并且在高维张量索引上比较麻烦。

float * image, * filtr, * result;
image  = (float *) aligned_alloc(64, size_image  * sizeof(float));
filtr  = (float *) aligned_alloc(64, size_filtr  * sizeof(float));
result = (float *) aligned_alloc(64, size_result * sizeof(float));

我们使用 (伪) 随机数初始化：

srand(0);
rand_vec(image, size_image);
rand_vec(filtr, size_filtr);

10.2. Direct 卷积的平凡算法#

我们曾经在第一篇文档的 极简 Python 实现 中给出 Direct 卷积的平凡算法的公式与实现，并在 最简单 C++ 实现 中展示了平凡算法的 (糟糕的) 效率。

这里运行代码的目的是生成作为参考的结果。

float * result_ref;
result_ref = (float *) aligned_alloc(64, size_result * sizeof(float));
for (int i = 0; i < size_result; ++i) result_ref[i] = 0;

auto start = chrono::steady_clock::now();

for (size_t i = 0; i < N; ++i)
for (size_t k = 0; k < OC; ++k)
for (size_t x = 0; x < OH; ++x)
for (size_t y = 0; y < OW; ++y)
for (size_t c = 0; c < IC; ++c)
for (size_t u = 0; u < 3; ++u)
for (size_t v = 0; v < 3; ++v)
    result_ref[((i * OC + k) * OH +   x) * OW +   y] += \
    image     [((i * IC + c) * IH + x+u) * IW + y+v] * \
    filtr     [((k * IC + c) *  3 +   u) *  3 +   v];

auto end = chrono::steady_clock::now();
chrono::duration<double> elapsed_seconds = end - start;
cout << "elapsed time: " << elapsed_seconds.count() * 1000 << " msec";

elapsed time: 71711.4 msec

10.3. Winograd \(F(6, 3)\) 优化策略概述#

10.3.1. Winograd \(F(6, 3)\) 算法回顾#

首先我们需要回顾 Winograd \(F(6, 3)\) 算法。该算法滤波前的卷积核大小是 \(3\)，滤波放大后的卷积核大小是 \(\mu = 6+2 = 8\)。下面通篇中，用斜体标注的矩阵的角标是完整的。该算法在最简单的拆分下，可以看作是

  1. 输入图像变换 (角标索引 \(i, c, \tilde x, \tilde y\)，其中 \(\tilde x\) 取值是 \(\{0, 6, 12, \cdots, H_\mathrm{in} - \mu = 50\}\)，\(\tilde y\) 取值是 \(\{0, 6, 12, \cdots, W_\mathrm{in} - \mu = 50\}\)；输入图像张量的另一种表示 \(d^{(\tilde x, \tilde y)}_{i,c,t,w} = d_{i,c,\tilde x+t,\tilde y+w}\))

    \[ V_{i,c,r,s}^{(\tilde x, \tilde y)} = \sum_t^\mu \sum_s^\mu B_{tr} d^{(\tilde x, \tilde y)}_{i,c,t,w} B_{ws} \;\; \text{or} \;\; \mathrm{V}_{i,c}^{(\tilde x, \tilde y)} = \mathrm{B}^\dagger \mathrm{d}^{(\tilde x, \tilde y)}_{i,c} \mathrm{B} \]

  2. 卷积核变换 (角标索引 \(k, c\))

    \[ U_{k,c,r,s} = \sum_u^K \sum_v^K G_{r,u} g_{k,c,u,v} G_{s,v} \;\; \mathrm{or} \;\; \mathrm{U}_{k,c} = \mathrm{G} \mathrm{g}_{k,c} \mathrm{G}^\dagger \]

  3. 数乘 (角标索引 \(i, k, \tilde x, \tilde y, r, s\))

    \[ M_{i,k,r,s}^{(\tilde x, \tilde y)} = \sum_c^{C_\mathrm{in}} U_{k,c,r,s} V_{i,c,r,s}^{(\tilde x, \tilde y)} \;\; \mathrm{or} \;\; \mathrm{M}_{i,k}^{(\tilde x, \tilde y)} = \sum_c^{C_\mathrm{in}} \mathrm{U}_{k,c} \odot \mathrm{V}_{i,c}^{(\tilde x, \tilde y)} \]

  4. 输出图像变换

    \[ Y_{i,k,\tilde x+a, \tilde y+b} = Y_{i,k,a,b}^{(\tilde x, \tilde y)} = \sum_r^\mu \sum_s^\mu A_{r,a} M^{(\tilde x, \tilde y)}_{i,k,r,s} A_{s,b} \;\; \mathrm{or} \;\; \mathrm{Y}_{i,k}^{(\tilde x, \tilde y)} = \mathrm{A}^\dagger \mathrm{M}^{(\tilde x, \tilde y)}_{i,k} \mathrm{A} \]

10.3.2. 优化策略#

对于整个卷积过程，或 Winograd 算法中，浮点计算数 FLOPs 最大的步骤一般应当是数乘步骤 (这应当是需要验证的，但这里我们假设如此)。因此，第三步数乘的优化尤为关键。

计算效率的基础优化大致分为两类情况：对浮点运算数的优化 (节省 CPU 运算时间)、以及对内存通信的优化 (节省 CPU 高级缓存、缓存到内存的通信时间)。对于 Winograd \(F(6,3)\) 算法而言，数乘运算次数是确定的。如果希望改进数乘算法，那么就需要使用更大的 Winograd 滤波；这当然是一种策略，但我们马上也会认识到这种做法的局限性。我们着重于内存通信的优化。

我们注意到，如果对待运算的张量不加以内存大小限制，那么内存通信就必须要在频率较低的 L3 缓存、甚至主内存空间完成。

  • 对于滤波后的卷积核 \(U_{k, c, r, s}\)，其维度是 \((C_\mathrm{out}, C_\mathrm{in}, \mu, \mu) = (256, 256, 8, 8)\)，因此其占用的内存空间是 16 MB，或 (一个浮点数为 32 bit 或 4 Byte)

    \[ 256 \times 256 \times 8 \times 8 \times 4 \, \text{Byte} = 16 \, \text{MB} \]

  • 对于变换后的输入图像 \(V_{i,c,r,s}^{(\tilde x, \tilde y)}\)，其维度是 \((N, C_\mathrm{in}, \mu, \mu, \tilde H, \tilde W) = (8, 256, 8, 8, 9, 9)\)，占用的内存空间是 40.5 MB。

我们用于测试算法的设备是 Intel Xeon Gold 6150 (4 sockets)，共 36 物理内核 (cores), 72 线程 (threads)。在这个设备上，我们程序能有效进行的并发数是物理内核数 36，而非线程数。一些细节参数是 (带宽由 Intel Advisor 给出)

缓存或内存

缓存大小

带宽

L1

32 kB / core

483 GB / sec·core

L2

1024 kB / core

228 GB / sec·core

L3

24.75 MB / 18 cores

213 GB / sec

DRAM

101 GB / sec

需要指出，L2 缓存的带宽是每个物理内核的速度，因此相比较 L3 带宽的效能提升是相当巨大的。同时 L2 缓存的大小也较大。而 L1 缓存的空间太小，要最大化利用 L1 缓存的难度比较大。因此，对内存通信的优化问题中，基于 L2 缓存优化是第一个、也是最重要的优化策略。

注意到变换后的卷积核 \(U_{k, c, r, s}\) 的占用空间相对较小、使用次数较多。因此我们可以考虑对该卷积核，依 L2 缓存大小，进行分批次计算。

具体来说，令 \(\tilde C, \tilde K\) 分别是单次分批处理时，变换后卷积矩阵 \(\mathrm{U}\) 的输入、输出通道大小。在我们的程序实现中，经过一些试错性尝试，认为效率比较高的做法是，每批次输入通道数是 \(\tilde C = 32\)，输出通道数 \(\tilde K = 64\)。在这种情形下，每批次数乘计算的 \(\mathrm{U}\) 矩阵的维度是 \((\tilde C, \tilde K, \mu, \mu) = (32, 84, 8, 8)\)，即 512 kB；该大小确实地控制在了 L2 缓存大小 1024 kB / core 以下。

为了较严格地用公式表达，我们定义矩阵 \(\mathrm{U}_{k,c}^{(\tilde k, \tilde c)} = \mathrm{U}_{\tilde k + k, \tilde c + c}\)。这里 \(\tilde k, \tilde c\) 的取值分别是 \(\{0, \tilde K, 2 \tilde K, \cdots, C_\mathrm{out} - \tilde K \}\) 和 \(\{0, \tilde C, 2 \tilde C, \cdots, C_\mathrm{out} - \tilde C \}\)，表示分批的批次；\(k \in [0, \tilde K), c \in [0, \tilde C)\) 则表示在每一个批次中卷积核矩阵的角标。

由此，我们可以比较清晰地写出我们所使用的基于 L2 缓存优化的 Winograd 算法。

winograd L2 batched algorithms

上述的算法过程看起来比最初提到的算法要臃肿。原始的算法中，输入、输出图像都只需要读取一次即可。但当前的算法中，输入图像会读取 \(C_\mathrm{out} / \tilde K = 4\) 次，而输出图像的内存则要经过 \(C_\mathrm{in} / \tilde C = 8\) 次写入。这看起来似乎是巨大的资源浪费；但为了高效地实现最耗时的数乘步骤，其余步骤中内存通信量的牺牲是值得的。

上面算法伪代码中，特意留出了第 4 行与第 8 行，表明单次用于数乘运算的变换后卷积核矩阵 \(\mathrm{U}^{(\tilde k, \tilde c)}_{k, c}\) 与变换后输入图像矩阵 \(\mathrm{V}^{(\tilde x, \tilde y, \tilde c)}_{i, c}\) 的内存占用大小。如前所述，\(\mathrm{U}\) 的内存占用是 512 kB，小于 L2 缓存。我们还会发现，对于 \(\mathrm{V}\)，其维度是 \((\tilde C, \mu, \mu) \rightarrow (32, 8, 8)\) 即 8 kB。这个大小也小于 L1 缓存的 32 kB。因此作为基于 L2 缓存优化的副产物，数乘运算也对 L1 缓存一定程度上友好。

10.4. Winograd \(F(6,3)\) 单步计算程序与复杂度分析#

10.4.1. 滤波变换：一般总结#

我们简单再回顾一下上面伪代码算法中出现的滤波变换：

  • 计算卷积核变换：\(\mathrm{U}^{(\tilde k, \tilde c)}_{k,c} {}^\dagger = \mathrm{G} (\mathrm{G} \mathrm{g}^{(\tilde k, \tilde c)}_{k,c})^\dagger\)

  • 计算输入图像变换：\(\mathrm{V}_{i,c}^{(\tilde x, \tilde y, \tilde c)} {}^\dagger = \mathrm{B}^\dagger (\mathrm{B}^\dagger \mathrm{d}^{(\tilde x, \tilde y, \tilde c)}_{i,c})^\dagger\)

  • 计算输出图像变换：\(\mathrm{Y}_{i,k}^{(\tilde x, \tilde y)} \mathrel{+}= \mathrm{A}^\dagger (\mathrm{A}^\dagger \mathrm{M}^{(\tilde x, \tilde y, \tilde c)}_{i,k} {}^\dagger)^\dagger\)

这三种变换有共同的特征：1) 一个数值确定的矩阵 (\(\mathrm{G}, \mathrm{B}^\dagger, \mathrm{A}^\dagger\)) 与数值可变的矩阵乘积；2) 上述结果转置；3) 上述数值确定的矩阵 (\(\mathrm{G}, \mathrm{B}^\dagger, \mathrm{A}^\dagger\)) 再次进行乘积。

那么在后续的实现中，就要考虑到 1) 矩阵转置的高效实现；上述涉及到的矩阵维度都不超过 \((\mu, \mu)\) 即 \((8, 8)\) 维度，因此我们也只着重考察 8x8 转置问题。2) 与数值确定的矩阵 (\(\mathrm{G}, \mathrm{B}^\dagger, \mathrm{A}^\dagger\)) 的乘积可以使用手写的、特化的程序，而不需要使用通用的矩阵乘法 (譬如 Level 3 Blas 的 SGEMM 等等)，从而最大程度上节约实际所需的浮点运算数。

在后续的文段中，为了方便，我们会统一将数值可变的矩阵记为 \(\mathrm{D}\)。

10.4.2. SIMD 与 Intrinsic 指令#

现在的 CPU 通常支持 SIMD (Single Instruction, Multiple Data) 机制 (一种向量化编程的模式)。对于 Skylake 系列的 CPU (支持 AVX512 指令集)，如果要进行普通的单个浮点数加法 \(b + c\) 或乘法 \(b \cdot c\)，那么需要一个汇编指令 addss 或 mulss。而执行向量长度为 16 的向量数乘与加法 \(\boldsymbol{a} \mathrel{+}= \boldsymbol{b} \odot \boldsymbol{c}\) 单浮点数运算 (Fused-Multiple-Add, FMA)，也只需要一个汇编指令 vfmadd***ps 即可。长度为 16 的 FMA 指令需要处理 16 次乘法与 16 次加法，即总共是 32 次加与乘法。而在 Skylake 系列上，FMA (32 次加与乘法)、单次加法、单次乘法单个指令的延迟 (latency) 与吞吐量 (throughput) 是完全一致的。因而若能合理地利用 SIMD 指令，运算的速度最快可以提升 32 倍！

在这份文档中，为了在一次指令下完成更多的计算任务，我们的所有计算过程基于 __m512 编写。__m512 是一种基于向量化 (Vectorization) 的类型；使用其的目的是尽量在单个指令下完成多个数据的计算；一个 __m512 向量可以储存 16 个单浮点数。在 C++ 本身的语言特性中，没有对其的规范；但对于大多数基于 x86 的 CPU，可以使用固有指令 (Intrinsic)，在 C 或 C++ 的高级语言级别进行编程。Intel Intrinsics Guide 非常完整地罗列了可用的 Intrinsics。

需要指出，尽管一般来说，一行 Intrinsic 对应一行 Assembly (最底层的汇编指令)；但 Intrinsic 应当只是给编译器推荐合适的 Assembly，而并不是要求编译器必须使用我们所希望的 Assembly。因而若要清楚地确定当前的计算机是如何实现一段计算过程，那么最好要从 Assembly 来看。同时，像 -O3, --march=native 等编译指令事实上也会对一般的程序 (不使用 Intrinsic 编程的程序) 进行向量化优化；因而对于相对简单的问题，只要代码写得足够清晰高效，不需要 Intrinsic 一样可以达到很高的效率。

在当前的问题中，出现的 Assembly 会有 (下表的 Latency 与 Throughput 数据取自于 Intel 所提供的 Skylake 系列；编译时加入 -S 选项可以生成汇编文件 *.s 以详细查看汇编代码)

Instruction

指令目的

Latency

Throughput

vmovaps, vmovups

内存移动

5~8

0.5~1

vaddps, vsubps, vmulps

加、减、乘运算

4

0.5

vfmadd***ps, vfmsub***ps

FMA 运算

4

0.5

vunpcklps, vunpckhps, vshufps

向量混合

1

1

vpermi2ps, vpermt2ps

向量重排

3

1

上述表格给予我们至少两个信息 (以 Skylake 为前提)：

  1. FMA 运算与加、减、乘法运算的耗时和延迟是一致的；因此在可以用 FMA 运算的地方，要尽量使用。这可以最大提升 2 倍的运算力。

  2. 内存移动的消耗通常比运算要更大。要尽可能减少内存移动。

10.4.3. __m512 下 8x8 转置的实现#

对于使用 __m512 向量类型，我们会发现一个问题：一个 __m512 向量可以储存的 float 类型数是 16；它不能直接用于 8x8 的转置。

在这里，由于当前问题所需要进行的矩阵转置数量很大，我们所使用的解决方案是，使用 8 个 __m512 向量，一次性处理两个矩阵转置问题。

下述函数 mm_transpose_8x8 的输入 row 是 __m512 类型的两个横向并排待转置的矩阵，输出 tr 是两个横向并排的结果矩阵。需要注意，输入的指令集向量 row 的数据会被更改。

/// +---+---+     +---+---+
/// |   |   | --> | T | T |
/// +---+---+     +---+---+
inline void mm_transpose_8x8(__m512 row[8], __m512 tr[8]) {
    const __m512i i0x20 = _mm512_set_epi32(033, 032, 031, 030, 013, 012, 011, 010, 023, 022, 021, 020, 003, 002, 001, 000);
    const __m512i i0x31 = _mm512_set_epi32(037, 036, 035, 034, 017, 016, 015, 014, 027, 026, 025, 024, 007, 006, 005, 004);
    tr[0] = _mm512_unpacklo_ps(row[0], row[1]);
    tr[1] = _mm512_unpackhi_ps(row[0], row[1]);
    tr[2] = _mm512_unpacklo_ps(row[2], row[3]);
    tr[3] = _mm512_unpackhi_ps(row[2], row[3]);
    tr[4] = _mm512_unpacklo_ps(row[4], row[5]);
    tr[5] = _mm512_unpackhi_ps(row[4], row[5]);
    tr[6] = _mm512_unpacklo_ps(row[6], row[7]);
    tr[7] = _mm512_unpackhi_ps(row[6], row[7]);
    row[0] = _mm512_shuffle_ps(tr[0], tr[2], _MM_SHUFFLE(1, 0, 1, 0));
    row[1] = _mm512_shuffle_ps(tr[0], tr[2], _MM_SHUFFLE(3, 2, 3, 2));
    row[2] = _mm512_shuffle_ps(tr[1], tr[3], _MM_SHUFFLE(1, 0, 1, 0));
    row[3] = _mm512_shuffle_ps(tr[1], tr[3], _MM_SHUFFLE(3, 2, 3, 2));
    row[4] = _mm512_shuffle_ps(tr[4], tr[6], _MM_SHUFFLE(1, 0, 1, 0));
    row[5] = _mm512_shuffle_ps(tr[4], tr[6], _MM_SHUFFLE(3, 2, 3, 2));
    row[6] = _mm512_shuffle_ps(tr[5], tr[7], _MM_SHUFFLE(1, 0, 1, 0));
    row[7] = _mm512_shuffle_ps(tr[5], tr[7], _MM_SHUFFLE(3, 2, 3, 2));
    tr[0] = _mm512_permutex2var_ps(row[0], i0x20, row[4]);
    tr[1] = _mm512_permutex2var_ps(row[1], i0x20, row[5]);
    tr[2] = _mm512_permutex2var_ps(row[2], i0x20, row[6]);
    tr[3] = _mm512_permutex2var_ps(row[3], i0x20, row[7]);
    tr[4] = _mm512_permutex2var_ps(row[0], i0x31, row[4]);
    tr[5] = _mm512_permutex2var_ps(row[1], i0x31, row[5]);
    tr[6] = _mm512_permutex2var_ps(row[2], i0x31, row[6]);
    tr[7] = _mm512_permutex2var_ps(row[3], i0x31, row[7]);
}

矩阵转置的演示效果如下所示。

// Initialize intrinsics
float a[128], b[16]; __m512 t[8], r[8];
for (size_t i = 0; i < 64; ++i) {
    a[i / 8 * 16 + i % 8] = i;
    a[i / 8 * 16 + i % 8 + 8] = i + 64;
}
for (size_t i = 0; i < 8; ++i) t[i] = _mm512_loadu_ps(&a[i * 16]);

printf("Original Matrix:\n");
for (size_t i = 0; i < 8; ++i) {
    _mm512_store_ps(&b[0], t[i]);
    for (size_t j = 0; j < 16; ++j) printf("%4.0f", b[j]);
    printf("\n");
}

// Transform 8x8 for intrinsics (t -> r)
mm_transpose_8x8(&t[0], &r[0]);
printf("\nTransposed Matrix (8x8):\n");
for (size_t i = 0; i < 8; ++i) {
    _mm512_store_ps(&b[0], r[i]);
    for (size_t j = 0; j < 16; ++j) printf("%4.0f", b[j]);
    printf("\n");
}

Original Matrix:
   0   1   2   3   4   5   6   7  64  65  66  67  68  69  70  71
   8   9  10  11  12  13  14  15  72  73  74  75  76  77  78  79
  16  17  18  19  20  21  22  23  80  81  82  83  84  85  86  87
  24  25  26  27  28  29  30  31  88  89  90  91  92  93  94  95
  32  33  34  35  36  37  38  39  96  97  98  99 100 101 102 103
  40  41  42  43  44  45  46  47 104 105 106 107 108 109 110 111
  48  49  50  51  52  53  54  55 112 113 114 115 116 117 118 119
  56  57  58  59  60  61  62  63 120 121 122 123 124 125 126 127

Transposed Matrix (8x8):
   0   8  16  24  32  40  48  56  64  72  80  88  96 104 112 120
   1   9  17  25  33  41  49  57  65  73  81  89  97 105 113 121
   2  10  18  26  34  42  50  58  66  74  82  90  98 106 114 122
   3  11  19  27  35  43  51  59  67  75  83  91  99 107 115 123
   4  12  20  28  36  44  52  60  68  76  84  92 100 108 116 124
   5  13  21  29  37  45  53  61  69  77  85  93 101 109 117 125
   6  14  22  30  38  46  54  62  70  78  86  94 102 110 118 126
   7  15  23  31  39  47  55  63  71  79  87  95 103 111 119 127

10.4.4. 将连续内存空间转换到可计算的指令集上#

这里还遇到一个问题。譬如对于这种情形：一个矩阵有 8x8 个元素，我们希望对其行向量进行加减操作。但对于 __m512 类型的向量，每个向量都可以放 16 个浮点数。因此连续内存下，两个 8x8 个元素的矩阵，储存方式其实是放在两个 4x16 的向量中。这样的存储方式会给计算带来些许麻烦。

为了使计算更为方便，我们可以将 2 个连续内存下的 8x8 矩阵进行重排，使得第一个矩阵在 8 个 __m512 的左侧、第二个矩阵在右侧。这样，向量的加法计算就可以在两个并排的 8x8 矩阵下容易完成了。

具体的做法是，对于连续内存到计算空间下的转换定义为 mm_transpose_8x16_row2col：

//   +-------+-------+     +-------+-------+
//   +       1       +     +       +       +
//   +-------+-------+ --> +   1   +   2   +
//   +       2       +     +       +       +
//   +-------+-------+     +-------+-------+
inline void mm_transpose_8x16_row2col(__m512 row[8], __m512 tr[8]) {
    const __m512i ihi = _mm512_set_epi32(027, 026, 025, 024, 023, 022, 021, 020, 007, 006, 005, 004, 003, 002, 001, 000);
    const __m512i ilo = _mm512_set_epi32(037, 036, 035, 034, 033, 032, 031, 030, 017, 016, 015, 014, 013, 012, 011, 010);
    tr[0] = _mm512_permutex2var_ps(row[0], ihi, row[4]);
    tr[1] = _mm512_permutex2var_ps(row[0], ilo, row[4]);
    tr[2] = _mm512_permutex2var_ps(row[1], ihi, row[5]);
    tr[3] = _mm512_permutex2var_ps(row[1], ilo, row[5]);
    tr[4] = _mm512_permutex2var_ps(row[2], ihi, row[6]);
    tr[5] = _mm512_permutex2var_ps(row[2], ilo, row[6]);
    tr[6] = _mm512_permutex2var_ps(row[3], ihi, row[7]);
    tr[7] = _mm512_permutex2var_ps(row[3], ilo, row[7]);
}

其使用效果是

// Initialize intrinsics
float a[128], b[16]; __m512 t[8], r[8];
for (size_t i = 0; i < 128; ++i) a[i] = i;
for (size_t i = 0; i < 8; ++i) t[i] = _mm512_loadu_ps(&a[i * 16]);

printf("Original Matrix:\n");
for (size_t i = 0; i < 8; ++i) {
    _mm512_store_ps(&b[0], t[i]);
    for (size_t j = 0; j < 16; ++j) printf("%4.0f", b[j]);
    printf("\n");
}

// Transform 8x16 row->col
mm_transpose_8x16_row2col(&t[0], &r[0]);
printf("\nTransposed Matrix (8x16, row->col):\n");
for (size_t i = 0; i < 8; ++i) {
    _mm512_store_ps(&b[0], r[i]);
    for (size_t j = 0; j < 16; ++j) printf("%4.0f", b[j]);
    printf("\n");
}

Original Matrix:
   0   1   2   3   4   5   6   7   8   9  10  11  12  13  14  15
  16  17  18  19  20  21  22  23  24  25  26  27  28  29  30  31
  32  33  34  35  36  37  38  39  40  41  42  43  44  45  46  47
  48  49  50  51  52  53  54  55  56  57  58  59  60  61  62  63
  64  65  66  67  68  69  70  71  72  73  74  75  76  77  78  79
  80  81  82  83  84  85  86  87  88  89  90  91  92  93  94  95
  96  97  98  99 100 101 102 103 104 105 106 107 108 109 110 111
 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127

Transposed Matrix (8x16, row->col):
   0   1   2   3   4   5   6   7  64  65  66  67  68  69  70  71
   8   9  10  11  12  13  14  15  72  73  74  75  76  77  78  79
  16  17  18  19  20  21  22  23  80  81  82  83  84  85  86  87
  24  25  26  27  28  29  30  31  88  89  90  91  92  93  94  95
  32  33  34  35  36  37  38  39  96  97  98  99 100 101 102 103
  40  41  42  43  44  45  46  47 104 105 106 107 108 109 110 111
  48  49  50  51  52  53  54  55 112 113 114 115 116 117 118 119
  56  57  58  59  60  61  62  63 120 121 122 123 124 125 126 127

如果希望从计算空间转换到连续内存，则反其道而行之。函数定义为 mm_transpose_8x16_col2row：

//   +-------+-------+     +-------+-------+
//   +       +       +     +       1       +
//   +   1   +   2   + --> +-------+-------+
//   +       +       +     +       2       +
//   +-------+-------+     +-------+-------+
inline void mm_transpose_8x16_col2row(__m512 row[8], __m512 tr[8]) {
    const __m512i ihi = _mm512_set_epi32(027, 026, 025, 024, 023, 022, 021, 020, 007, 006, 005, 004, 003, 002, 001, 000);
    const __m512i ilo = _mm512_set_epi32(037, 036, 035, 034, 033, 032, 031, 030, 017, 016, 015, 014, 013, 012, 011, 010);
    tr[0] = _mm512_permutex2var_ps(row[0], ihi, row[1]);
    tr[1] = _mm512_permutex2var_ps(row[2], ihi, row[3]);
    tr[2] = _mm512_permutex2var_ps(row[4], ihi, row[5]);
    tr[3] = _mm512_permutex2var_ps(row[6], ihi, row[7]);
    tr[4] = _mm512_permutex2var_ps(row[0], ilo, row[1]);
    tr[5] = _mm512_permutex2var_ps(row[2], ilo, row[3]);
    tr[6] = _mm512_permutex2var_ps(row[4], ilo, row[5]);
    tr[7] = _mm512_permutex2var_ps(row[6], ilo, row[7]);
}

其使用效果是

// Transform 8x16 row->col
mm_transpose_8x16_col2row(&r[0], &t[0]);
printf("\nTransposed Matrix (8x16, col->row):\n");
for (size_t i = 0; i < 8; ++i) {
    _mm512_store_ps(&b[0], t[i]);
    for (size_t j = 0; j < 16; ++j) printf("%4.0f", b[j]);
    printf("\n");
}

Transposed Matrix (8x16, col->row):
   0   1   2   3   4   5   6   7   8   9  10  11  12  13  14  15
  16  17  18  19  20  21  22  23  24  25  26  27  28  29  30  31
  32  33  34  35  36  37  38  39  40  41  42  43  44  45  46  47
  48  49  50  51  52  53  54  55  56  57  58  59  60  61  62  63
  64  65  66  67  68  69  70  71  72  73  74  75  76  77  78  79
  80  81  82  83  84  85  86  87  88  89  90  91  92  93  94  95
  96  97  98  99 100 101 102 103 104 105 106 107 108 109 110 111
 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127

10.4.5. 输入图像变换#

输入图像变换过程为

\[ V^\dagger = B^\dagger (B^\dagger D)^\dagger \]

这个过程中的关键步骤是 \(T = B^\dagger D\)。尽管矩阵乘法的实现非常简单，但会产生大量不必要的浮点运算。因此，这类矩阵乘法运算要手动将实现。

若记向量 \(T_i, D_i\) 分别是矩阵 \(T, D\) 的第 \(i\) 行，那么

\[\begin{split} \begin{align*} T_0 &= D_0 + 5.25 \times (D_4 - D_2) - D_6 \\ T_1 &= \big( D_2 - 4.25 \times D_4 + D_6 \big) + \big( D_1 - 4.25 \times D_3 + D_5 \big) \\ T_2 &= \big( D_2 - 4.25 \times D_4 + D_6 \big) - \big( D_1 - 4.25 \times D_3 + D_5 \big) \\ T_3 &= \big( 0.25 \times D_2 - 1.25 \times D_4 + D_6 \big) + \big( 0.5 \times D_1 - 2.5 \times D_3 + 2 \times D_5 \big) \\ T_4 &= \big( 0.25 \times D_2 - 1.25 \times D_4 + D_6 \big) - \big( 0.5 \times D_1 - 2.5 \times D_3 + 2 \times D_5 \big) \\ T_5 &= \big( 4 \times D_2 - 5 \times D_4 + D_6 \big) + \big( 2 \times D_1 - 2.5 \times D_3 + 0.5 \times D_5 \big) \\ T_6 &= \big( 4 \times D_2 - 5 \times D_4 + D_6 \big) - \big( 2 \times D_1 - 2.5 \times D_3 + 0.5 \times D_5 \big) \\ T_7 &= D_7 + 5.25 \times (D_3 - D_5) - D_1 \end{align*} \end{split}\]

程序的实现为 transform_BtD_6x3。其运算是通过输入 8 行指令向量 D、输出 8 行指令向量 BtD 实现的。对于 GCC 编译器，其当前版本对指令集的支持程度可能好于 ICC 编译器；对于指令集加、减、乘法和 FMA 运算，不需要使用 Intrinsic (譬如 _mm512_fmadd_ps 这类又长又难于看懂的指令函数)，编译器可以正确地编译出高效的 SIMD 汇编。

inline void transform_BtD_6x3(const __m512 D[8], __m512 BtD[8]) {
    __m512 s0, s1;
    BtD[0] = D[0] + 5.25f * (D[4] - D[2]) - D[6];
    s0 = D[1] - 4.25f * D[3] + D[5];
    s1 = D[2] - 4.25f * D[4] + D[6];
    BtD[1] = s0 + s1;
    BtD[2] = s1 - s0;
    s0 = 0.5f * D[1] - 2.5f * D[3] + 2.f * D[5];
    s1 = D[6] + 0.25f * D[2] - 1.25f * D[4];
    BtD[3] = s0 + s1;
    BtD[4] = s1 - s0;
    s0 = 2.f * D[1] - 2.5f * D[3] + 0.5f * D[5];
    s1 = D[6] + 4.f * D[2] - 5.f * D[4];
    BtD[5] = s0 + s1;
    BtD[6] = s1 - s0;
    BtD[7] = D[7] - D[1] + 5.25f * (D[3] - D[5]);
}

在实际的程序实现中，我们需要一次性对两个输入图像矩阵进行变换。这两个矩阵未必需要在相连的内存空间中；但输出时最好需要在相连的内存实现。

下述程序 perform_image_transform 将两个输入图像 8x8 矩阵 im1, im2 代入，输出连续内存空间的 8x16 的指令集 v 的函数。该函数同时需要传入图像矩阵的首行维度 IW \(W_\mathrm{in}\)。

inline void perform_image_transform(const float im1[], const float im2[], __m512 v[], int IW) {
    __m512 zmm_a[8], zmm_b[8];
    // Initialize __m512 of two input images
    for (int i = 0; i < 8; ++i) {
        zmm_b[i] = _mm512_loadu_ps(&im1[i * IW]);
        zmm_b[i] = _mm512_insertf32x8(zmm_b[i], _mm256_loadu_ps(&im2[i * IW]), 1);
    }
    // Perform B.T @ D
    transform_BtD_6x3(zmm_b, zmm_a);
    // Perform (B.T @ D).T
    mm_transpose_8x8(zmm_a, zmm_b);
    // Perform V.T = B.T @ (B.T @ D).T
    transform_BtD_6x3(zmm_b, zmm_a);
    // Consequential memory for two transformed images
    mm_transpose_8x16_col2row(zmm_a, v);
}

10.4.6. 卷积核变换#

卷积核变换过程为

\[ U^\dagger = G (G D)^\dagger \]

这个过程中关键的步骤是 \(T = GD\)。该过程涉及到的输入 \(D\) 或者 \((GD)^\dagger\) 是 3 行的矩阵，但输出是 8 行的矩阵。

\[\begin{split} \begin{align*} T_0 &= D_0 \\ T_1 &= -2/9 \times (D_0 + D_2) - 2/9 \times D_1 \\ T_2 &= -2/9 \times (D_0 + D_2) + 2/9 \times D_1 \\ T_3 &= (1/90 \times D_0 + 2/45 \times D_2) + 1/45 \times D_1 \\ T_4 &= (1/90 \times D_0 + 2/45 \times D_2) - 1/45 \times D_1 \\ T_5 &= (32/45 \times D_0 + 8/45 \times D_2) + 16/45 \times D_1 \\ T_6 &= (32/45 \times D_0 + 8/45 \times D_2) - 16/45 \times D_1 \\ T_7 &= D_2 \end{align*} \end{split}\]

程序的实现为 transform_GD_6x3。其运算是通过输入 3 行指令集向量 D、输出 8 行指令集向量 GD 实现的。

inline void transform_GD_6x3(const __m512 D[3], __m512 GD[8]) {
    __m512 s0, s1;
    GD[0] = D[0];
    GD[7] = D[2];
    s0 = -2.f/9.f * (D[0] + D[2]);
    s1 = -2.f/9.f * D[1];
    GD[1] = s0 + s1;
    GD[2] = s0 - s1;
    s0 = 1.f/90.f * D[0] + 2.f/45.f * D[2];
    s1 = 1.f/45.f * D[1];
    GD[3] = s0 + s1;
    GD[4] = s0 - s1;
    s0 = 32.f/45.f * D[0] + 8.f/45.f * D[2];
    s1 = 16.f/45.f * D[1];
    GD[5] = s0 + s1;
    GD[6] = s0 - s1;
}

下述程序 perform_filter_transform 将两个卷积核 3x3 矩阵 f[0:9], f[9:18] 代入 (这里要求两个卷积核是内存连续的)，输出连续内存空间的 8x16 的指令集 zmm_u 的函数。

inline void perform_filter_transform(const float f[], __m512 zmm_u[]) {
    // Initialize __m512 of two input filters (convolution kernels)
    __m512 zmm_a[8], zmm_b[8];
    for (int i = 0; i < 3; ++i) {
        zmm_b[i] = _mm512_loadu_ps(&f[3 * i]);
        zmm_b[i] = _mm512_insertf32x8(zmm_b[i], _mm256_loadu_ps(&f[9 + 3 * i]), 1);
    }
    // Perform G @ D
    transform_GD_6x3(zmm_b, zmm_a);
    // Perform (G @ D).T
    mm_transpose_8x8(zmm_a, zmm_b);
    // Perform U.T = G @ (G @ D).T
    transform_GD_6x3(zmm_b, zmm_a);
    // Consequential memory for two transformed filters
    mm_transpose_8x16_col2row(zmm_a, zmm_u);
}

10.4.7. 输出图像变换#

输出图像变换过程比较类似于输入图像变换：

\[ Y = A^\dagger (A^\dagger D)^\dagger \]

这个过程中关键的步骤是 \(T = A^\dagger D\)。该过程涉及到的输入 \(D\) 或者 \((GD)^\dagger\) 是 8 行的矩阵，输出是 6 行的矩阵。

\[\begin{split} \begin{align*} T_0 &= (D_1 + D_2) + (D_3 + D_4) + (D_5 + D_6) + D_0 \\ T_2 &= (D_1 + D_2) + 4 \times (D_3 + D_4) + \frac{1}{4} \times (D_5 + D_6) \\ T_4 &= (D_1 + D_2) + 16 \times (D_3 + D_4) + \frac{1}{16} \times (D_5 + D_6) \\ T_1 &= (D_1 - D_2) + 2 \times (D_3 - D_4) + \frac{1}{2} \times (D_5 - D_6) \\ T_3 &= (D_1 - D_2) + 8 \times (D_3 - D_4) + \frac{1}{8} (D_5 - D_6) \\ T_5 &= (D_1 - D_2) + 32 \times (D_3 - D_4) + \frac{1}{32} (D_5 - D_6) + D_7 \end{align*} \end{split}\]

程序的实现为 transform_AtD_6x3。其运算是通过输入 8 行指令集向量 D、输出 6 行指令集向量 AtD 实现的。

inline void transform_AtD_6x3(const __m512 D[8], __m512 AtD[6]) {
    __m512 s0, s1, s2;
    s0 = D[1] + D[2];
    s1 = D[3] + D[4];
    s2 = D[5] + D[6];
    AtD[0] = s0 + s1 + s2 + D[0];
    AtD[2] = s0 + 4.f * s1 + 0.25f * s2;
    AtD[4] = s0 + 16.f * s1 + 0.0625f * s2;
    s0 = D[1] - D[2];
    s1 = D[3] - D[4];
    s2 = D[5] - D[6];
    AtD[1] = s0 + 2.f * s1 + 0.5f * s2;
    AtD[3] = s0 + 8.f * s1 + 0.125f * s2;
    AtD[5] = s0 + 32.f * s1 + 0.03125f * s2 + D[7];
}

下述程序 perform_store_transform 将两个横向并列的矩阵 \(M^\dagger\) 通过向量 zmm_m 代入，随后将图像输出到两个图像的指针 r1, r2 上。需要注意，输出的图像是 6x6 矩阵，因此不能简单地直接使用 _mm256_storeu_ps 将 8 个浮点数写入内存 (会将两个无效数据误写入可能存放有意义数据的位置上)，而是要使用带遮罩的向量存储方式。

inline void perform_store_transform(__m512 zmm_m[8], float *r1, float *r2, int OW) {
    __m512 zmm_a[8], zmm_b[8];
    unsigned char mask = 63;
    mm_transpose_8x16_row2col(zmm_m, zmm_b);
    transform_AtD_6x3(zmm_b, zmm_a);
    mm_transpose_8x8(zmm_a, zmm_b);
    transform_AtD_6x3(zmm_b, zmm_a);
    for (int i = 0; i < 6; ++i) {
        _mm256_mask_storeu_ps(&r1[i * OW], mask, _mm512_extractf32x8_ps(zmm_a[i], 0) + _mm256_loadu_ps(&r1[i * OW]));
        _mm256_mask_storeu_ps(&r2[i * OW], mask, _mm512_extractf32x8_ps(zmm_a[i], 1) + _mm256_loadu_ps(&r2[i * OW]));
    }
}

10.4.8. 数乘#

我们先回顾到数乘的公式表达是

\[ \mathrm{M}_{i,k}^{(\tilde x, \tilde y, \tilde c)} {}^\dagger = \sum_c^{\tilde C} \mathrm{U}^{(\tilde k, \tilde c)}_{k,c} {}^\dagger \odot \mathrm{V}_{i,c}^{(\tilde x, \tilde y, \tilde c)} {}^\dagger \]

回顾到之前的伪代码，其中的 \(i, \tilde x, \tilde y, \tilde k, \tilde c\) 是已经确定的数值；那么上述角标复杂的表达式可以简化为

\[ \mathrm{M}_{k} {}^\dagger = \sum_c^{\tilde C} \mathrm{U}_{k,c} {}^\dagger \odot \mathrm{V}_{c} {}^\dagger \]

该过程还需要角标 \(k\) 的参与。下述的程序 perform_mult 中，

  • u1, u2 分别是两个 \(k\) 取值下的 \(\mathrm{U}_{k,c}^\dagger\) 或者写为张量元素的形式 \(U_{k,c,s,r}\) (维度 \((c,s,r) \rightarrow (\tilde C, \mu, \mu)\))；

  • v 就是 \(\mathrm{V}_{c}^\dagger\) 张量，维度与 u1 或 u2 相同；

  • sizeIC 是输入通道数的分割大小 \(\tilde C\)；

  • zmm_m 是两个 \(k\) 取值下的 \(\mathrm{M}_{k} {}^\dagger\)，维度是 \((2, \mu, \mu)\) 即 \((2, 8, 8)\)；这两个 8x8 矩阵分别储存在两个 4x16 的指令集向量中。

执行 perform_mult 程序时，还需要对 \(k\) 进行循环。

inline void perform_mult(const __m512 u1[], const __m512 u2[], const __m512 v[], __m512 zmm_m[8], int sizeIC) {
    for (int i = 0; i < 8; ++i)
        zmm_m[i] = _mm512_setzero_ps();
    for (int ci = 0; ci < sizeIC; ++ci) {
        for (int i = 0; i < 4; ++i) {
            zmm_m[i] += u1[0] * v[0];
            zmm_m[i + 4] += u2[0] * v[0];
            ++u1; ++u2; ++v;
        }
    }
}

10.5. Winograd \(F(6,3)\) 总程序#

有了所有单步程序后，我们可以回归到伪代码的运算过程了。由于整体的 Winograd 伪代码难以再分割出子过程了，因此下面需要用一段完整的代码实现最后统合的一步了。

对程序作一些补充说明：

  • 变量 hintOC, hintIC 分别是输出通道数的分割大小 \(\tilde K\) 与输入通道数分割大小 \(\tilde C\) 的初始设定值。这可以作为程序的常值超参数进行调整，用于确定哪一种分割会使程序运行地更快。但之所以说是“初始设定值”，是因为有可能会遇到输出通道数为 96、输入通道数为 3 等特殊情况。具体分割时需要考虑到边界情况。

  • 所有子程序都需要通过强制 inline 嵌入到 winconv 主程序中；否则效率可能会受到严重影响。

  • 程序最一开始需要对输出图像置零；这一步在 \(C_\mathrm{in}\) 较小时是相对耗时的。可以通过并行置零的方式提升效率，实测会比 memset 等做法要快很多。

  • 变量 startOC, startIC 分别是 \(\tilde k, \tilde c\)；变量 x_, y_ 分别是 \(\tilde x, \tilde y\)。

  • 下述程序的 // 注释中的 line 是指上面伪代码的行号。

  • 下述程序尚没有对 \(C_\mathrm{in}\) 为奇数、\(H_\mathrm{in}, W_\mathrm{in}\) 模 6 不余 2 的边界情况作实现。关于这些边界情况，请参考实际程序 winograd_f6x3.cpp 的做法。

constexpr int hintOC = 64;
constexpr int hintIC = 32;

void winconv(const float *__restrict__ image, const int IH,
             const int IW, const int IC, const float *__restrict__ filter,
             const int OC, const int N, float *__restrict__ result) {
    const int OH = IH - 2;
    const int OW = IW - 2;
    const int TH = ceildiv(OH, 6);
    const int TW = ceildiv(OW, 6);

    const int sliceOC = min(OC, hintOC);
    const int sliceIC = min(IC, hintIC);

    const int size_result = N * OC * OH * OW;
    
    // line 1: zero initialize output image Y
#pragma omp parallel
#pragma omp for simd aligned(result) schedule(static)
    for (int i = 0; i < size_result; ++i) result[i] = 0;
    
    // line 2: for tilde(k), tilde(c)
    for (int startOC = 0; startOC < OC; startOC += sliceOC) {
        Range rOC(startOC, min(startOC + sliceOC, OC));
        for (int startIC = 0; startIC < IC; startIC += sliceIC) {
            Range rIC(startIC, min(startIC + sliceIC, IC));

// line 3: declare parallel for every CPU cores
#pragma omp parallel default(shared)
            {
                // line 4, 8: allocate U in L2-cache, V in L1-cache
                __m512 V[rIC.size() * 4];
                __m512 U[rOC.size() * rIC.size() * 4];
                
                // line 5: compute U, transformation of convolutional kernel
                for (int k = rOC.start; k < rOC.end; ++k) {
                    for (int c = rIC.start; c < rIC.end; c += 2) {
                        int ki = k - rOC.start, ci = c - rIC.start;
                        const float *f = &filter[(k * IC + c) * 9];
                        __m512 *u = &U[(ki * rIC.size() + ci) * 4];
                        perform_filter_transform(f, u);
                    }
                }

// line 6: embrassingly parallel following for loop
//         adding `collapse` directive if N is not comparable to available number of CPU cores
#pragma omp for schedule(static)
                // line 7: for i, tilde(x), tilde(y)
                for (int i = 0; i < N; ++i) {
                    for (int x_ = 0; x_ < TH; ++x_) {
                        for (int y_ = 0; y_ < TW; ++y_) {
                            int x = x_ * 6, y = y_ * 6;
                            
                            // line 9: compute V, transformation of input image
                            for (int c = rIC.start; c < rIC.end; c += 2) {
                                int ci = c - rIC.start;
                                const float *im1 = &image[((i * IC + c) * IH + x) * IW + y];
                                const float *im2 = &im1[IW * IH];
                                __m512 *zmm_v = &V[ci * 4];
                                perform_image_transform(im1, im2, zmm_v, IW);
                            }
                            
                            // line 10: compute M, perform multiplication
                            // line 11: compute Y, transformation of output image
                            for (int k = rOC.start; k < rOC.end; k += 2) {
                                int ki = k - rOC.start;
                                __m512 *zmm_u1 = &U[ki * rIC.size() * 4], *zmm_u2 = &zmm_u1[rIC.size() * 4];
                                __m512 *zmm_v = V;
                                __m512 zmm_m[8];
                                perform_mult(zmm_u1, zmm_u2, zmm_v, zmm_m, rIC.size());
                                float *r1 = &result[((i * OC + k) * OH + x) * OW + y];
                                float *r2 = &r1[OH * OW];
                                perform_store_transform(zmm_m, r1, r2, OW);
                            }
                        }
                    }
                }
            }
        }
    }
}

我们可以用下述程序运行是否正确，并考察效率。尽管当前的 Jupyter xeus-cling 引擎未必能达到很高效率，但我们可以看见程序运行时间从 Naive Direct 的大约 70 sec 锐减到大约 100 ms，效率提升可以达到约 700 倍。要注意到若只考虑 Winograd 算法相对 Direct 算法的算术运算数的减少量，对于 Winograd \(F(6,3)\) 也不可能超过 5 倍。这确实能体现基于 L2 缓存的程序效率优化的重要意义了。

auto start = chrono::steady_clock::now();

winconv(image, IH, IW, IC, filtr, OC, N, result);

auto end = chrono::steady_clock::now();
chrono::duration<double> elapsed_seconds = end - start;
cout << "elapsed time: " << elapsed_seconds.count() * 1000 << " msec";

elapsed time: 108.482 msec

allclose(result, result_ref, size_result)

true

10.6. 实机测试#

在这一节中，我们会对我们的程序进行效率测评。

测评用设备与参数

  • CPU 为 Intel Xeon Gold 6154 (x4)；

    • 物理内核 (core) 数 72，NUMA 节点数 4；

    • L1d 32 kB / core, L1i 32 kB / core, L2 1024 kB / core；

    • L3 24.75 MB；

  • GCC 10.2.0；

  • 编译选项 -fopenmp -O3 -march=native。

关于具体的编译过程，参考 CMakeLists.txt。编译所用的程序为 run_winograd_f6x3。

运行的网络为完整的 16 层 VGG16 网络；网络参数的定义文件在 vgg16.conf。其中 Batch 大小 \(N = 64\)。以 10 次连续计算的平均时间记为运行时间。可能出于测评的体量较小、内存对齐、预热效应等可能的影响，效率测评结果会有一定波动。

算法的效率以平均 GFLOPS 给出。GFLOPS 可以看作是每秒执行的算术次数；计算方式是通过 Direct Convolution 确定，而非是当前的 Winograd 算法。

10.6.1. 参数 \(\tilde K, \tilde C\) 的选择#

我们先前说道，输出通道分批数 \(\tilde K\)、输入通道分批数 \(\tilde C\) 设置的大小应当要使矩阵 \(\mathrm{U}^{(\tilde k, \tilde c)}_{k, c}\) (维度 \((\tilde K, \tilde C, \mu, \mu)\)) 契合 L2 缓存大小。下述表格就是调整 \(\tilde K\) (hintOC) 与 \(\tilde C\) (hintIC) 时所给出的 GFLOPS；每列最高效率的数值将加粗。计算在 64 核并行下完成。下述表格的数据是五次平行运行后取的最大值。

\(\tilde C \text{\\} \tilde K\)

8

16

24

32

48

64

96

128

8

1596

2465

2891

3251

3394

3603

3712

3477

16

2305

3413

3844

4210

4521

4674

4686

4766

24

2594

3762

4171

4678

4727

5236

5171

4327

32

2574

3756

4270

4734

5094

5389

4774

2824

48

2600

3595

4306

4557

4747

4365

2615

1894

64

2674

3703

4280

4266

3980

2676

1942

-

96

2682

3731

3978

3887

2574

1961

-

-

128

2732

3711

3419

2514

1857

-

-

-

从上表中，我们发现 \(\tilde K = 64\), \(\tilde C = 32\) 确实是最佳情况，算法效率达到 5389 GFLOPS。

但这就遇到另一个问题：为何不能是 \(\tilde K = 32\), \(\tilde C = 64\) 呢？在这种情况下，每批次 \(\mathrm{U}^{(\tilde k, \tilde c)}_{k, c}\) 大小仍然是 512 kB 并小于 L2 缓存大小。这其中有几种无法断言的可能性：

  • 一般来说，高速缓存最好能最大化地利用。但或许每批次 \(\mathrm{U}^{(\tilde k, \tilde c)}_{k, c}\) 不能占用太大的缓存大小。因为图片输入、输出、转换等过程都需要 L2 缓存介入；如果其它繁杂的数据流被限制住了，那么就算与 \(\mathrm{U}^{(\tilde k, \tilde c)}_{k, c}\) 计算密集型任务算得再快，还是得经常等其它数据通过小水管载入到高速缓存中。所以尽管 L2 缓存是 1024 kB / core，但占用 512 kB / core 是比较合适的。这可能解释了为何 \(\tilde K = 96\), \(\tilde C = 32\) 效率相对较低的原因。

  • 我们先前也提及，在 \(i, \tilde x, \tilde y, \tilde c\) 角标确定的情况下，每批次 \(\mathrm{V}^{(\tilde x, \tilde y, \tilde c)}_{i, c}\) 的内存占用是 \((\tilde C, \mu, \mu)\) 大小；当 \(\tilde C = 32\) 时，可以使得 \(\mathrm{V}^{(\tilde x, \tilde y, \tilde c)}_{i, c}\) 的内存占用为 8 kB，小于 L1d 缓存的 32 kB。基于许多 \(\tilde K\) 的取值下 \(\tilde C\) 都在 32 附近有较高效率，我尝试推测：如果 \(\tilde C\) 再大一些，就可能因为 L1d 缓存不能容纳其它计算的需求，而对效率有显著影响。

10.6.2. 与 Intel DNNL 的效率比较#

我们也将程序与 Intel DNNL 进行横向对比。使用 64 core 并行；网络结构相同的层会对 GFLOPS 取平均。Intel DNNL 是指 oneAPI 2022.2 的机器学习程序库。对比情况如下 (网络详情也可以参考 [2] Table 3)。效率以 GFLOPS 为单位呈现。

Layer

Depth

\((C_\mathrm{in} \times H_\mathrm{in} \times W_\mathrm{in})\)

\(C_\mathrm{out}\)

DNNL Direct

DNNL Winograd

My Winograd

conv(1.1)

1

3 x 224 x 224

64

160

352

828

conv(1.2)

1

64 x 224 x 224

64

2423

4572

5332

conv(2.1)

1

64 x 112 x 112

128

3160

4458

5384

conv(2.2)

1

128 x 112 x 112

128

4676

6344

5836

conv(3.1)

1

128 x 56 x 56

256

5312

5183

5686

conv(3.2)

3

256 x 56 x 56

256

6524

4283

6565

conv(4.1)

1

256 x 28 x 28

512

5933

3399

5769

conv(4.2)

4

512 x 28 x 28

512

7264

5466

5329

conv(5)

5

512 x 14 x 14

512

5112

2588

4578

VGG16

4420

4250

5497

可以见到，我们的实现并非在每个网络上都超过了 DNNL。

  • 可能是受限于 Winograd 算法本身，在网络的最后三四层，即图像很小、卷积核较大的情况，使用直接卷积计算有可能效率更高。

  • 我们也存在 conv(2.2) 效率没有超过 DNNL Winograd 的效率。

  • DNNL Winograd 的实现可能基于 \(F(2,3)\) 和 \(F(4,3)\)；我们上述的实现是 \(F(6,3)\)。

  • DNNL 的库文件很大；将程序载入内存的时间也考虑在了测评过程中。以及 DNNL 使用了 JIT 技术，有可能 JIT 处理时间也有一定影响。

我们也指出，该上述的代码思路并非是决赛阶段所使用的思路。Winograd \(F(6, 3)\) 有办法可能更快。

10.6.3. 并行效率#

下图呈现了我们程序在不同核数下的并行效率。可以认为并行效率相对可观。

也必须指出，上面的程序是对 Batch 数 \(N\) 作简单并行的；如果 Batch 数并不是很友好的数字 (譬如 80)，或者 Batch 数为 64 却被要求在 48 核机器上并行，那么该程序的并行效率应当不会很好。

Parallel Efficiency

10.6.4. Roofline 图#

Intel Advisor (advixe-cl) 可以绘制 Roofline 图。Roofline 图是可以直观分析程序片段的内存负载量与计算指令调用数量。它同时还可以交互式地给出程序片段的运行时间、以及联结程序与汇编代码。可以是相当强大的代码效率分析工具。

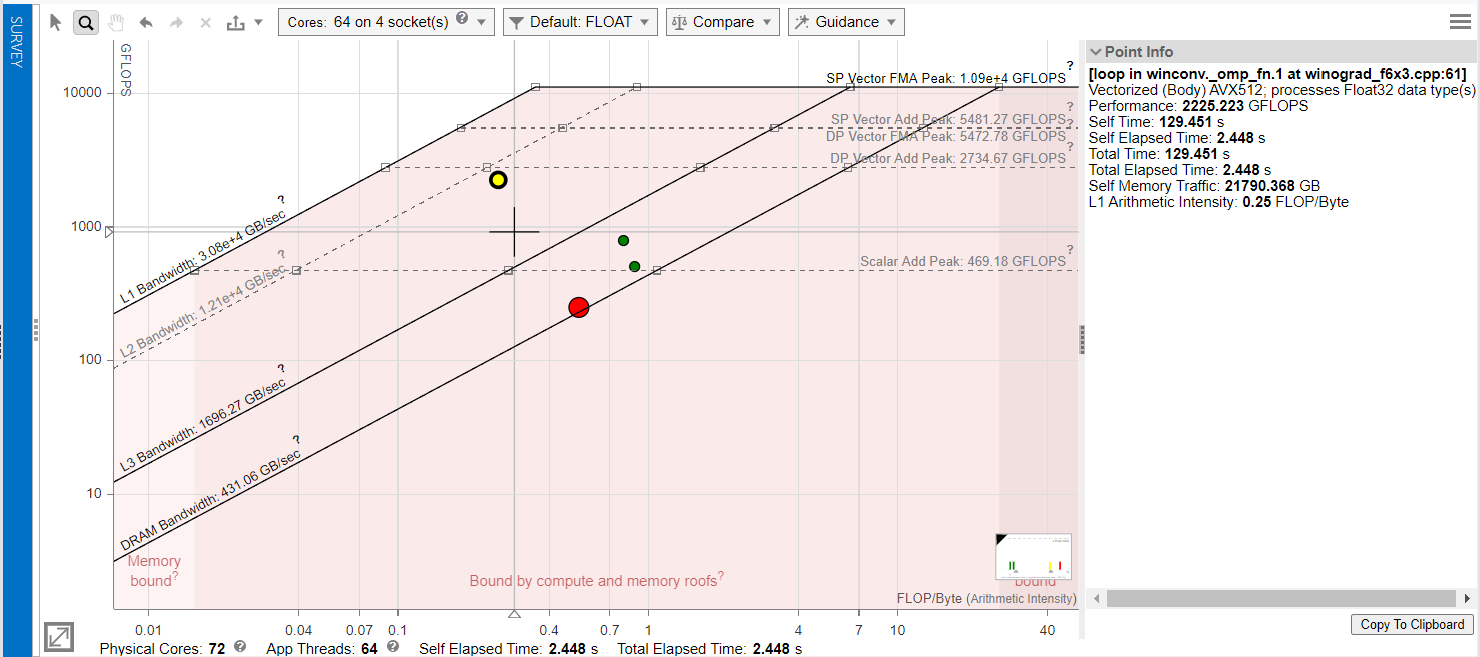
下图是对 64 core 并行的 Winograd VGG16 程序运行过程所绘制的 Roofline 图。目前我还未完全了解其中的功能；但通过与下述 Roofline 图的简单交互，应当可以确定，

  • 黄色点是数乘运算点，运行耗时约 129 sec；该程序所调用的内存通讯的带宽接近 L2 带宽，确实符合我们程序设计的预期。

  • 两个绿色点分别是输入图像变换与卷积核变换，分别耗时 36 sec 与 33 sec。

  • 红色点是输出图像变换与内存写入过程，耗时约 154 sec。事实上，我们编写的程序的最耗时步骤，对于整个 VGG16 网络而言其实是输出图像部分。这也是 Winograd 算法的特点：尽管可以降低数乘部分运算的次数，但其余部分的转换与读写量的增加制约了效率。

roofline

10.7. 后记与致谢#

我曾经一直都只是高性能计算的使用者；计算化学目前毫无疑问地消耗着着大量的计算资源。尽管也会进行程序编写，但实际上至多是调库玩家；先前并不了解高性能计算的逻辑，甚至不了解高速缓存和汇编代码为何物。

感谢赛方九坤投资、以及队长强宜澄。因为这场竞赛，我从无到有、确实地一窥高性能计算的一角，也有不少收获。对于提升与改进程序效率，除了低标度 (Lower-Scaling/Complexity) 算法外，确实地可以多一个视角来看待。也再次感谢赛方提供的自主饮食、奖励和周边 0w0；以及强哥大腿，他的努力促成了我们小队在决赛阶段获得第二名的佳绩，我也能沾光 =w=。希望强哥后面的求学之路能顺利。

正因为计算化学耗费的资源量巨大；由同时在我狭隘的目之所及的化学出身从业者内 (我认为 Southern Methodist University 的 Devin Matthews 应是这类从业者的范例)，较少有对底层计算机架构有深入理解和强编程能力 (就像 Winograd 算法这类写得真高效的话，譬如冠军代码或我们小队队长在决赛时所用的代码，会又 hard 又 lengthy 又 dirty >.< 能力确实需要很强)；因此，高性能计算在计算化学中的应用前景和提升空间或许是可预见的。化学问题经常会遇到大量且复杂的张量缩并；受制于自己的眼界，要如何具体地借助高性能计算提升计算化学算法，与我而言还需要一些思考。

写这篇文档的时候已经博六了，毕业课题还没搞定。确实可以慢慢想哈哈 >.<

赛题中还包含了关于 HDF5 的读存效率问题。在我先前的项目中，确实遇到需要与磁盘进行大量交互的问题 (将电子积分或激发张量存入硬盘的二阶梯度算法实现)。对 HDF5 赛题的学习，也确实料及了关于如何合理测评基于硬盘的算法的效率的方式，以及一定条件下合理地利用 chunk 提升硬盘读写的效率的思路。

事实上参赛时段的前后，因为一些外因，我多少有些负面情绪；这次比赛确实给予我以一些信心；也要感谢各同学老师的宽容。以及感谢课题组闲置计算资源的支持。

还有许多问题值得进取，还有许多技术可以玩味。以后如果有时间，还蛮想在类 GPU 上多些了解。

对基于 CPU 的高性能计算初步学习，LAFF 系列课程 的第三个课程 LAFF-On Programming for High Performance 相信是不错的初步材料。这个学习材料是在决赛后发现的。它介绍了比较基础的指令集级别的矩阵乘法 DGEMM 性能优化思路与实现。

文档目录