2. Autograd (2):深度前馈网络——前向传播与反向传播#
创建时间:2019-12-20
这一份文档将会回顾比较多的内容。
第一段中,我们会使用以向量模长为学习目标的模型训练过程,来作最为简单的深度网络模型:多层感知的学习与热身。
第二段中,我们会了解网络中的参数如何调取与浏览,并且解释多层感知模型本质上几乎就是普通的矩阵与向量运算,学习前向传播过程。
网络参数导数是模型训练过程中非常重要的参考。第三段中,我们会了解网络参数关于损失函数的导数,学习反向传播过程。
import torch
import torch.nn as nn
import numpy as np
from IPython.display import Image
torch.set_printoptions(precision=5, sci_mode=False, linewidth=120)
torch.Tensor.backward.__defaults__ = (None, True, False)
2.1. PyTorch 多层感知 (MLP) 学习向量模长的简易例子#
2.1.1. 小样本学习#
相信绝大多数脚本砖工在入门深度学习的时候,都是拿一些现实的问题,譬如 MNIST 数据集或 Iris 数据集来作训练。这可以加深砖工们学习的积极性与目的性,训练的结果也确实可以有效地泛化 (不严格地说,泛化类似于实用化),固然不错。
但这里尝试用另一种方式来作入门级说明。我们拿一种事实上不太适合深度学习的问题来举例,不管是从问题的意义上还是实用性的角度上。这个问题是用多层感知 (multi-layer perceptron) 模型,学习固定长度 (5 长度) 向量的模长。但这样一个问题非常容易用数学的方式作定义,其训练集与学习目标都是完全可重复、不需要任何先验的知识就可以构建;并且不需要脚本砖工最关心和头疼的数据集处理 (特征向量处理) 的过程。
在 PyTorch 中,这样一个简单的模型 model 可以通过下述简单的 layer 堆叠得到:
torch.random.manual_seed(0)
model = nn.Sequential(nn.Linear(5, 4), nn.ReLU(), nn.Linear(4, 3), nn.ReLU(), nn.Linear(3, 1))
model
Sequential(
(0): Linear(in_features=5, out_features=4, bias=True)
(1): ReLU()
(2): Linear(in_features=4, out_features=3, bias=True)
(3): ReLU()
(4): Linear(in_features=3, out_features=1, bias=True)
)
关于上述每一段代码的意义,后文会作更详细的描述。下面的图片就是对上述模型的一个简单描述:
Image(filename="assets/vector_to_norm.png", width=515)
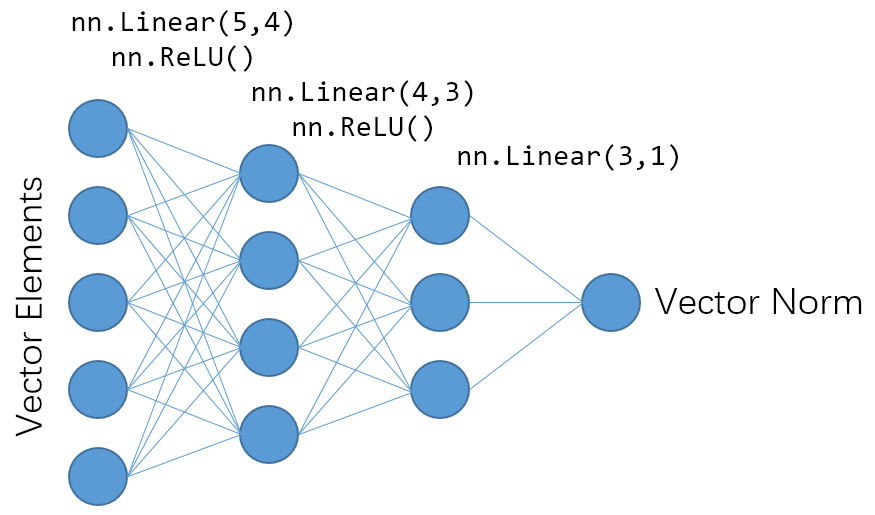
因此,上述网络的输入是 5 长度的向量,通过 MLP 过程,即两层神经网络层 (线性层与激活层的叠加) 与一层线性层后,得到长度为 1 的向量模长。第一层的神经元数量为 4,第二层则为 3。
网络构建完毕后,我们可以构建用于训练的数据集 X。
X的第一维度为 6,意指总共有 6 个数据点用于训练;X的第二维度为 5,意指作为特征 (Feature) 或者说数据点的向量长度为 5。
X = torch.randn(6, 5)
X
tensor([[ 0.25963, -0.17396, -0.67875, 0.93826, 0.48887],
[-0.67309, 0.87283, 1.05536, -0.00479, -0.51807],
[-0.30670, -1.58099, 1.70664, -0.44622, 2.08196],
[ 1.70671, 2.38037, -1.12560, -0.31700, -1.09247],
[-0.08519, -0.09335, -0.76071, -1.59908, 0.01849],
[-0.75043, 0.18541, 0.62114, 0.63818, -0.24600]])
我们可以很容易地构建该数据集下的真实值 t。真实值就是对数据集 X 表示数据点的维度 (第二维度) 取模长就得到:
t = X.norm(dim=1, keepdim=True)
t
tensor([[1.29526],
[1.61155],
[3.16858],
[3.33766],
[1.77540],
[1.20463]])
在当前简单的问题中,MLP 的意义就是一个拟合映射:
我们定义 y 是 MLP 模型下,输入数据 X 给出的结果。
我们会希望在参数学习的过程中,y 渐渐地接近真实结果 t。但在完全没有进行训练的状况下,我们应该会预期这两者的差距会相当大 (我们暂时拿 L1 损失函数来衡量误差):
y = model(X)
float(nn.L1Loss()(y, t))
1.9639991521835327
若要让 MLP 模型的结果 y 接近真实结果 t,我们就需要对模型的参数进行优化。下面的代码使用了以下的优化参数:
优化器使用 SGD (stochastic gradient descent) (在一般的深度学习问题中,通常大家会更推荐 Adam 优化器);
学习率始终为 0.02;
使用 L1 作为损失函数;
学习过程中使用梯度下降次数为 1001 次。
但需要指出,实际的深度学习的优化过程的参数是需要一些经验性的手动调整,以及引入验证集等降低泛化误差的做法。下面的代码只是非常简单的实例而已。
optimizer = torch.optim.SGD(model.parameters(), 0.02)
def train(model, X, t, optimizer):
y = model(X)
loss = nn.L1Loss()(y, t)
optimizer.zero_grad()
loss.backward()
optimizer.step()
return loss
for epoch in range(0, 1001):
loss = train(model, X, t, optimizer)
if epoch % 200 == 0:
print("Loss in epoch {:4d}: {:10.6f}".format(epoch, loss))
Loss in epoch 0: 1.963999
Loss in epoch 200: 0.397570
Loss in epoch 400: 0.049674
Loss in epoch 600: 0.098072
Loss in epoch 800: 0.103638
Loss in epoch 1000: 0.021809
这就完成了一次 MLP 的学习!我们可以看看现在模型作用在训练集上得到的结果 y:
model(X)
tensor([[1.24895],
[1.53482],
[3.02538],
[3.18011],
[1.70085],
[1.18437]], grad_fn=<AddmmBackward>)
你应该会认为这已经比较接近真实的目标模长值 t 了吧。
从刚才训练过程的输出中,我们应当知道训练集的误差大约在 0.02 左右。但这个模型 model 是否真的能用于预测任意的长度为 5 的向量的模长呢?答案是不仅否定的,而且刚才的模型甚至会比随机的预测还要糟糕!
下面的代码是取了足够大样本数量 (\(1,048,576 = 1024^2\)) 来作测试集 XX_test,并取另一个取自同一分布的 1,048,576 数量的长度为 5 的向量集合 Xr_test 作为随机向量。我们可以经验地认为,对一个向量模长的随机的猜测,可以是与测试集相同分布的另一个随机向量的模长。
如果一个理想的机器学习模型应当要比随机猜测要好许多。但下面的代码显示,随机猜测的误差为 0.78 左右,但模型 model 所给出的误差却是 0.91 左右。这意味着模型给出的结果甚至不如瞎蒙!
torch.random.manual_seed(0)
XX_test = torch.randn(1048576, 5)
Xr_test = torch.randn(1048576, 5)
print("Loss for random guess: {:10.6f}".format(nn.L1Loss()(XX_test.norm(dim=1, keepdim=True), Xr_test.norm(dim=1, keepdim=True))))
print("Loss for trained model: {:10.6f}".format(nn.L1Loss()(model(XX_test), XX_test.norm(dim=1, keepdim=True))))
Loss for random guess: 0.776423
Loss for trained model: 0.911286
一般来说,对这种现象的解释是,模型的参数较多,而训练集 X 的样本数量只有 6 个,因此会发生相当强的过拟合现象。简单粗暴地说来,就是模型会强烈地喜好接近训练集出现的 6 个样本的数据点,而不能很好地处理不太像训练集的数据点。
2.1.2. 大样本学习#
解决上述过拟合问题的一种解决方案是提高训练集数据量。现在我们重启一个从结构上完全等价,但参数的选取可以不同的模型 model_large。我们更换一个数据集:这次使用 1024 个样本作为数据集 X_large 来学习;并且使用以下的优化参数:
优化器使用 Adam;
学习率从 0.5 降低到 1e-5,降低的标准为连续 5 次 epoch 损失函数大于最低一次 epoch 损失函数值时,学习率降低到 0.9 倍;
使用 L1 作为损失函数;
学习过程中使用梯度下降次数为 1001 次。
torch.random.manual_seed(0)
model_large = nn.Sequential(nn.Linear(5, 4), nn.ReLU(), nn.Linear(4, 3), nn.ReLU(), nn.Linear(3, 1))
X_large = torch.randn(1024, 5)
t_large = X_large.norm(dim=1, keepdim=True)
optimizer = torch.optim.Adam(model_large.parameters(), .5)
scheduler = torch.optim.lr_scheduler.ReduceLROnPlateau(optimizer, mode="min", factor=0.9, patience=5, min_lr=1e-5)
def train_with_scheduler(model, X, t, scheduler):
y = model(X)
loss = nn.L1Loss()(y, t)
scheduler.optimizer.zero_grad()
loss.backward()
scheduler.optimizer.step()
scheduler.step(loss)
return loss
for epoch in range(0, 1001):
loss = train_with_scheduler(model_large, X_large, t_large, scheduler)
if epoch % 200 == 0:
print("Loss in epoch {:4d}: {:10.6f}".format(epoch, loss))
Loss in epoch 0: 2.000235
Loss in epoch 200: 0.344131
Loss in epoch 400: 0.308635
Loss in epoch 600: 0.307540
Loss in epoch 800: 0.307498
Loss in epoch 1000: 0.307497
对于上述学得的模型 model_large,我们发现其训练集上的误差约为 0.31,明显比小样本学习中的 0.02 要大许多;但在相同的测试集中,其误差却降低到 0.35 左右。这意味着 model_large 尽管仍然不能很好地预测向量的模长,但至少已经比随机猜测好许多。
print("Loss for random guess: {:10.6f}".format(nn.L1Loss()(XX_test.norm(dim=1, keepdim=True), Xr_test.norm(dim=1, keepdim=True))))
print("Loss for trained model: {:10.6f}".format(nn.L1Loss()(model_large(XX_test), XX_test.norm(dim=1, keepdim=True))))
Loss for random guess: 0.776423
Loss for trained model: 0.352113
在这种模型下,训练集与测试集的误差都不算太小但比较接近。一般认为这种情况已经有效地解决过拟合的效应,但存在相当严重的欠拟合效应。欠拟合效应反映的是模型本身的缺陷。
在这个例子中,这意味着 model_large 的参数不论如何学习,恐怕都无法作出有效的预测。一般来说会有效的解决方案可以是增大模型的大小 (反映在增加 MLP 神经元数量与层的数量),或干脆更换一套模型框架。
如何解决当前例子的欠拟合问题,不在这个文档的讨论范畴之内。
2.2. PyTorch 普通前馈网络的定义#
2.2.1. 段落目标:重复模型过程#
刚才我们花了不少精力,除了展示一个比较简单易行、但比较完整的深度学习流程之外,更重要的目的是说明了这篇文档的模型与数据。
后面的文档中,我们将会拿上面提到过的小样本模型 model 与数据集 X,来探讨 PyTorch 中 MLP 层具体是怎样计算,以及如何进行自动求导以更新参数表。这一段中我们先会解决前一个问题。我们的目标是,对于任何学习过最基础矩阵运算的人,都可以很轻易地理解到在给定参数的情况下,MLP 的前向传播过程不同于很多机器学习模型,在本质上仅仅是由非常简单的矩阵运算构成的。
在解决问题前,我们先将模型换为没有经过训练的状况。这么做的目的单纯地是为了让梯度变得大一些,以便后面比较有效的定性与定量分析。
torch.random.manual_seed(0)
model = nn.Sequential(nn.Linear(5, 4), nn.ReLU(), nn.Linear(4, 3), nn.ReLU(), nn.Linear(3, 1))
我们代入的训练集是 (6, 5) 的矩阵 X \(\mathbf{X}\);其第一维度为数据点数量,第二维度为特征向量长度。
X = torch.randn(6, 5)
X
tensor([[ 0.25963, -0.17396, -0.67875, 0.93826, 0.48887],
[-0.67309, 0.87283, 1.05536, -0.00479, -0.51807],
[-0.30670, -1.58099, 1.70664, -0.44622, 2.08196],
[ 1.70671, 2.38037, -1.12560, -0.31700, -1.09247],
[-0.08519, -0.09335, -0.76071, -1.59908, 0.01849],
[-0.75043, 0.18541, 0.62114, 0.63818, -0.24600]])
在模型的作用下,得到的结果是 (6, 1) 的矩阵向量 y \(\mathbf{y}\),其第一维度为数据点数量。
y = model(X)
y
tensor([[0.05652],
[0.11903],
[0.10917],
[0.10579],
[0.10462],
[0.11395]], grad_fn=<AddmmBackward>)
我们的目标是用普通的、容易理解的矩阵过程重新描述 layer(X)。
2.2.2. 模型参数#
模型 model 的定义是通过参数给出的。这些参数在 PyTorch 中以字典的形式储存在 state_dict 方法下:
param = model.state_dict()
type(param)
collections.OrderedDict
这意味着这些参数是可以被读取的。由于这个模型并不庞大,我们可以打出所有的参数数值以及它们在字典中对应的键值来。我们还可以同时计算出这个模型的参数总量为 43。
parameter_number = 0
for name, tensor in param.items():
print("------")
print("KEY:", name)
print("shape:", tuple(tensor.shape))
print(tensor)
parameter_number += torch.prod(torch.tensor(tensor.shape))
print("======")
print("Parameter number:", int(parameter_number))
------
KEY: 0.weight
shape: (4, 5)
tensor([[-0.00335, 0.23990, -0.36808, -0.32912, -0.17225],
[ 0.11992, -0.00886, 0.35459, -0.03969, 0.11834],
[-0.13515, -0.08791, -0.42724, -0.29618, -0.18435],
[ 0.01657, 0.17680, 0.26834, -0.30318, -0.19474]])
------
KEY: 0.bias
shape: (4,)
tensor([ 0.16244, 0.37136, -0.09204, 0.33466])
------
KEY: 2.weight
shape: (3, 4)
tensor([[-0.08059, 0.05291, 0.45274, -0.46384],
[-0.31477, -0.12658, -0.19490, 0.43200],
[-0.32409, -0.23017, -0.34932, -0.46828]])
------
KEY: 2.bias
shape: (3,)
tensor([-0.29187, 0.42980, 0.22311])
------
KEY: 4.weight
shape: (1, 3)
tensor([[ 0.27983, 0.03036, -0.29600]])
------
KEY: 4.bias
shape: (1,)
tensor([0.09768])
======
Parameter number: 43
如果我们希望取出其中第一个矩阵 0.weight,我们可以用下述代码:
param["0.weight"]
tensor([[-0.00335, 0.23990, -0.36808, -0.32912, -0.17225],
[ 0.11992, -0.00886, 0.35459, -0.03969, 0.11834],
[-0.13515, -0.08791, -0.42724, -0.29618, -0.18435],
[ 0.01657, 0.17680, 0.26834, -0.30318, -0.19474]])
使用 model.state_dict() 是比较标准的取出参数表的方法;我们之后为了能对参数进行导数计算,这里换用 model.named_parameters() 取出参数,并使用其它变量名替代其中的参数:
param = {}
for i in model.named_parameters():
param[i[0]] = i[1]
W_0, b_0 = param["0.weight"], param["0.bias"]
W_2, b_2 = param["2.weight"], param["2.bias"]
W_4, b_4 = param["4.weight"], param["4.bias"]
现在我们要解决如下的几个问题。
第一个问题是,键值的名称是如何被定义的。我们现在先回头看一下模型 model 是如何定义的:
model
Sequential(
(0): Linear(in_features=5, out_features=4, bias=True)
(1): ReLU()
(2): Linear(in_features=4, out_features=3, bias=True)
(3): ReLU()
(4): Linear(in_features=3, out_features=1, bias=True)
)
这就意味着,在 PyTorch 中,程序认定这个模型当前是 5 层 (而不是我们刚才提到的 MLP 的 2 层神经元的层数);其中第 0, 2, 4 层是线性层,1, 3 层是 ReLU 激活层。一般来说,一层神经元是指一层线性层叠加一层激活层;因此我们会说第一层神经元对应 model 的 0, 1 层,而第二层神经元对应 model 的第 2, 3 层。之后我们通常在提到“层”的时候,指的是程序中出现的 5 层。
其中具有参数的层只有线性层。W_0 表示的是第 0 层的权重 \(\mathbf{W}^0\),而 b_0 表示第 0 层的偏置 \(\mathbf{b}^0\)。第 2, 4 层类推。留意在这篇文档中,上标数字并不代表矩阵或向量的幂运算。
第二个问题是,每个参数值的维度是如何被定义的。
我们仍然需要回头看一下 model 的定义。以第 0 层为例,其输入特征长度 in_features 为 5,这与 X \(\mathbf{X}\) 的维度是相同;而其输出特征长度 out_features 为 4。另一个例子是最后一层即第 4 层,其输出特征长度 out_features 为 1,这与 y \(\mathbf{y}\) 的维度是相同。
对于任何线性层而言,其权重矩阵的维度为 (out_features, in_features);其偏置向量的维度为 (out_features, )。以第 0 层为例,
W_0.shape
torch.Size([4, 5])
b_0.shape
torch.Size([4])
关于权重矩阵与偏置向量,它们的作用将会马上在下一段介绍。
2.2.3. 线性层#
现在我们简单地了解一下第 0 层线性层的作用。实际上,线性层的作用是相当简单的:
上面的记号中,X_0 \(\mathbf{X}^0\) 表示第 0 层输出矩阵,X \(\mathbf{X}\) 表示第 0 层输入矩阵 (恰好为数据集),W_0 \(\mathbf{W}^{0}\) 表示第 0 层作为线性层的权重矩阵,b_0 \(\mathbf{b}^0\) 表示第 0 层作为线性层的偏置向量。上标 \(\mathrm{T}\) 表示矩阵转置。
X_0 = X @ param["0.weight"].T + param["0.bias"]
X_0
tensor([[-0.02335, 0.18398, -0.18986, -0.25360],
[ 0.07644, 0.59601, -0.43176, 0.86336],
[-1.05575, 1.21783, -0.89241, 0.23785],
[ 1.43460, 0.03912, 0.24424, 0.79060],
[ 0.94343, 0.15788, 0.72290, 0.59383],
[-0.18687, 0.44553, -0.41596, 0.37610]], grad_fn=<AddBackward0>)
但上述矩阵的表示相对来说不太直观;一种相对来说直观的方式可以是 (但不是标准的表示方法,只是作者写多了化学反应式自然会生成的一种习惯)
对于第 2, 4 层线性层,其过程是非常类似的:
2.2.4. 激活层#
MLP 的线性层一般就是普通的矩阵乘法,但激活层的选取可以较为丰富。一种典型与常用的激活层是 ReLU (Rectified Linear Unit),其定义非常简单:
因此,若我们记 X_0 \(\mathbf{X}^0\) 表示第 0 层输出矩阵,X_1 \(\mathbf{X}^0\) 表示第 1 层输出矩阵;那么
若联合线性层,其比较直观的表示方式为
对于程序的实现上,X_1 可以表示为
X_1 = torch.max(X_0, torch.tensor(0.))
X_1
tensor([[0.00000, 0.18398, 0.00000, 0.00000],
[0.07644, 0.59601, 0.00000, 0.86336],
[0.00000, 1.21783, 0.00000, 0.23785],
[1.43460, 0.03912, 0.24424, 0.79060],
[0.94343, 0.15788, 0.72290, 0.59383],
[0.00000, 0.44553, 0.00000, 0.37610]], grad_fn=<MaxBackward2>)
2.2.5. 总结#
现在我们可以写出 model 模型下,从 \(\mathbf{X}\) 到 \(\mathbf{y}\) 的流程:
若要写出每一步的详细过程,则可以是
我们将上述矩阵的计算操作结果记作 X_4 \(\mathbf{X}^4\),而仍然将 model(X) 的结果记作 y \(\mathbf{y}\)。我们可以发现这两者是完全等价的:
X_0 = X @ param["0.weight"].T + param["0.bias"]
X_1 = torch.max(X_0, torch.tensor(0.))
X_2 = X_1 @ param["2.weight"].T + param["2.bias"]
X_3 = torch.max(X_2, torch.tensor(0.))
X_4 = X_3 @ param["4.weight"].T + param["4.bias"]
X_4
tensor([[0.05652],
[0.11903],
[0.10917],
[0.10579],
[0.10462],
[0.11395]], grad_fn=<AddBackward0>)
y
tensor([[0.05652],
[0.11903],
[0.10917],
[0.10579],
[0.10462],
[0.11395]], grad_fn=<AddmmBackward>)
如果我们希望在一个公式内解决一切与 \(\mathbf{X}\) 到 \(\mathbf{y}\) 的映射,我们可以写作
X_4 = torch.max(torch.max(
X @ param["0.weight"].T + param["0.bias"],
torch.tensor(0.)) @ param["2.weight"].T + param["2.bias"],
torch.tensor(0.)) @ param["4.weight"].T + param["4.bias"]
X_4
tensor([[0.05652],
[0.11903],
[0.10917],
[0.10579],
[0.10462],
[0.11395]], grad_fn=<AddBackward0>)
至此,我们已经成功地用简单的矩阵运算还原了 PyTorch 封装过的 MLP 模型 model 了。这是可以是一个比较典型的模型重复的标准途径,也将会对文档第三部分了解模型的反向传播过程有重要的意义。
2.3. MLP 参数导数#
2.3.1. 被求导对象#
这里我们就以这个非常短小、但是需要使用链式法则进行反向传播的 MLP 模型 model 进行分析。我们的目标是与 PyTorch 的 Autograd 的结果进行核对。但我们在上一份文档中提到,任何函数的导数都必须转化为标量的导数;即使输出并非是标量,也必须乘以与输出相同维度的张量并作求和得到变量。
对于当前的问题而言,作为标量的值是输出 y \(\mathbf{y}\) 与真实值 t \(\mathbf{t}\) 的 L1 损失函数值 loss \(\mathrm{loss}\):
loss = nn.L1Loss()(y, t)
loss
tensor(1.96400, grad_fn=<L1LossBackward>)
这一段的分析都是基于 loss 的导数得到。对该值的导数可以通过下述方式得到:
model.zero_grad()
loss.backward()
print("grad of W_0"); print(W_0.grad)
print("grad of b_0"); print(b_0.grad)
print("grad of W_2"); print(W_2.grad)
print("grad of b_2"); print(b_2.grad)
print("grad of W_4"); print(W_4.grad)
print("grad of b_4"); print(b_4.grad)
grad of W_0
tensor([[ 0.00151, 0.00503, -0.00132, -0.00306, -0.00254],
[-0.00285, 0.00299, 0.00823, -0.01116, -0.00508],
[ 0.00160, 0.00226, -0.00186, -0.00189, -0.00106],
[ 0.00024, -0.00386, -0.00327, 0.00378, -0.00053]])
grad of b_0
tensor([ 0.00478, -0.00751, 0.00197, -0.01093])
grad of W_2
tensor([[ 0.00000, 0.00000, 0.00000, 0.00000],
[-0.01242, -0.01336, -0.00489, -0.01448],
[ 0.00000, 0.00908, 0.00000, 0.00000]])
grad of b_2
tensor([ 0.00000, -0.03036, 0.04933])
grad of W_4
tensor([[ 0.00000, -0.41996, -0.03013]])
grad of b_4
tensor([-1.])
2.3.2. 第 4 层参数导数:非参数矩阵引入#
在所有的参数中,最容易求的导数在最后一层。我们将 loss \(\mathrm{loss}\) 写为第 2 层参数的函数:
(X_3 @ W_4.T + b_4 - t).abs().sum() / t.shape[0]
tensor(1.96400, grad_fn=<DivBackward0>)
但从公式的表达角度上,上面的表达式不太容易被求导。在此,我们引入第 5 层非参数矩阵 l_5 \(\mathbf{l}^5 = \mathrm{dim} (\mathbf{y})^{-1} \mathrm{sgn} (\mathbf{y} - \mathbf{t})\),那么
或表示为矩阵元的形式,
上式中出现的 \(0\) 表示该维度恰好为 1 维。
l_5 = (y - t).sign() / y.shape[0]
l_5.shape
torch.Size([6, 1])
l_5.T @ (X_3 @ W_4.T + b_4 - t)
tensor([[1.96400]], grad_fn=<MmBackward>)
根据上面公式的表述,我们就可以比较容易地给出关于 \(\mathbf{W}^{4, \mathrm{T}}\) 的导数
或矩阵元的形式
我们可以将其 gW_4 与 PyTorch 自动导数给出的 W_4.grad 进行比对:
gW_4 = l_5.T @ X_3
torch.allclose(gW_4, W_4.grad)
True
但这里需要指出,由于 \(\mathbf{b}^4\) 作为偏置矩阵的维度与其它矩阵不太相同,因此在求梯度时,需要对 \(\mathbf{l}^{5, \mathrm{T}}\) 的第一维度,或者说对表示数据点数量的维度求和:
我们可以将其 gb_4 与 PyTorch 自动导数给出的 b_4.grad 进行比对:
gb_4 = l_5.T.sum(dim=-1)
torch.allclose(gb_4, b_4.grad)
True
2.3.3. 第 2 层参数导数:链式法则#
第二层参数的导数会复杂不少。如果我们把 loss \(\mathrm{loss}\) 写为第 2 层参数的函数:
l_5.T @ (nn.ReLU()(X_1 @ W_2.T + b_2) @ W_4.T + b_4 - t)
tensor([[1.96400]], grad_fn=<MmBackward>)
如果要尝试对 \(\mathbf{W}^{2}\) 或 \(\mathbf{b}^2\) 求导,我们又会遇到与刚才第四层导数相同的问题,即如何对 \(\mathrm{ReLU}\) 求导。我们引入第 3 层非参数矩阵 l_3 \(\mathbf{l}^3 = \mathrm{sgn}^+ (\mathbf{X}^{2})\):
或表示为矩阵元的形式,
其中,记号 \(\mathrm{sgn}^+\) 表示正值取 1,负值取 0:
上面的计算过程中,矩阵 elementwise 乘法与普通的矩阵乘法的运算优先级是相同的。
sgn_pos = lambda t: torch.max(t.sign(), torch.tensor(0.))
l_3 = sgn_pos(X_2)
l_3.shape
torch.Size([6, 3])
l_5.T @ (l_3 * (X_1 @ W_2.T + b_2) @ W_4.T + b_4 - t)
tensor([[1.96400]], grad_fn=<MmBackward>)
我们固然可以对上式直接求关于 \(\mathbf{W}^{2}\) 参数的导数得到 gW_2,并与 PyTorch 自动求导给出的 W_2.grad 进行比对:
或
gW_2 = W_4.T @ l_5.T * l_3.T @ X_1
torch.allclose(gW_2, W_2.grad)
True
但我们可以有更为精妙的做法 (或者说思考方法)。注意到我们可以将 \(\mathrm{loss}\) 看成关于 \(\mathbf{X}^3\) 的函数,而 \(\mathbf{X}^3\) 又可以看作是关于 \(\mathbf{W}^2\) 的函数:
或
那么,我们就可以分别写出导数
我们定义 \(\frac{\partial \mathrm{loss}}{\partial X_{ij}^3}\) 在程序中表示为 gX_3。依据链式法则,我们就可以给出
拿上式与 PyTorch 自动求导给出的 W_2.grad 进行比对也能得到正确的结果:
gX_3 = l_5 @ W_4
gW_2 = gX_3.T * l_3.T @ X_1
torch.allclose(gW_2, W_2.grad)
True
而对于 \(\mathbf{b}^2\) 的导数 gb_2 的情况也会非常类似:
gb_2 = (gX_3.T * l_3.T).sum(dim=-1)
torch.allclose(gb_2, b_2.grad)
True
我们也许在这个例子中没有感受到链式法则的意义;即使不使用链式法则,程序的复杂性也没有增大许多。但对于 \(\mathbf{W}^0\) 与 \(\mathbf{b}^0\),使用链式法则的意义就会表现出来。
2.3.4. 第 0 层参数导数:反向传播#
上面一小段中,在求导过程中我们使用了一次链式法则。下面我们会比较系统地,从头回顾,将问题一步一步拆分,从而获得第 0 层参数 \(\mathbf{W}^0\) 与 \(\mathbf{b}^0\) 的导数。
上述的表示在写程序时可能是方便的,但在分析时,容易会对维度的信息把握得不太好。我们在此将下标明确地写出:
其中的第 1, 3, 5 层引入了非参数矩阵,它们的定义为
l_1 = sgn_pos(X_0)
l_3 = sgn_pos(X_2)
l_5 = y.shape[0]**-1 * (y - t).sign()
我们的目标是第 0 层参数导数 \(\mathbf{W}^0\) 与 \(\mathbf{b}^0\),但我们的被求导对象 \(\mathrm{loss}\) 在第 5 层。反向传播的一种解读方式是,导数的求取是从最后层向前传播。那么我们一层一层地对导数进行求取。
第 5 层 gX_4 \(\frac{\partial \mathrm{loss}}{\partial X^4_{i0}}\)
gX_4 = l_5
第 4 层 gX_3 \(\frac{\partial \mathrm{loss}}{\partial X^3_{ij}}\)
gX_3 = gX_4 @ W_4
第 3 层 gX_2 \(\frac{\partial \mathrm{loss}}{\partial X^2_{ij}}\)
gX_2 = gX_3 * l_3
第 2 层 gX_1 \(\frac{\partial \mathrm{loss}}{\partial X^1_{ik}}\)
gX_1 = gX_2 @ W_2
第 1 层 gX_0 \(\frac{\partial \mathrm{loss}}{\partial X^0_{ik}}\)
gX_0 = gX_1 * l_1
第 0 层
gW_0 \(\frac{\partial \mathrm{loss}}{\partial W^0_{kl}}\)
gW_0 = gX_0.T @ X
torch.allclose(gW_0, W_0.grad)
True
gb_0 \(\frac{\partial \mathrm{loss}}{\partial b^0_{k}}\)
gb_0 = gX_0.sum(dim=0)
torch.allclose(gb_0, b_0.grad)
True
至此我们已经成功地使用了反向传播的方法,对最难求解的 \(\mathbf{W}^0\) 与 \(\mathbf{b}^0\) 的参数进行了导数求取。这样一个过程可以是非常清晰与规范化的。
对于该模型更简单的其它参数,或者对于层数更多的 MLP 网络,使用完全相同的方式也能生成所有的导数。
我们知道,深度网络的参数优化过程通常是梯度下降的衍生方法。如果知道了这些参数的导数量,我们至少相信可以很自然地写出一个 naive 梯度下降优参的程序,实现深度网络的学习。
