9. 卷积神经网络推理 (2):Winograd 卷积的纯 Python 实现#
公开时间:2022-01-03
备注
该工作是第五届 Ubiquant Challenge 量化新星挑战赛|并行程序设计竞赛的初赛入围相关工作。该工作在【天之孔】队长强宜澄的牵头下完成。
这份文档是 Winograd 算法的介绍与说明。原题是使用 Winograd 算法高效实现 \(3 \times 3\) 卷积核神经网络的推理过程;我们将在之后的文档再对原题进行讨论。
警告
文档作者当前工作 (计算化学理论的双杂化泛函分支) 与该文档所使用的应用或算法都毫无干系。文档除了卷积网络本身,大多数知识都是现学的,因此可能会在叙述中存在基本性错误。
import numpy as np
import itertools
这是应用与实现文档,我们不对卷积网络或 Winograd 算法作原理性的叙述与证明,也不讨论卷积网络的有效性。我们只考察卷积核大小为 \(3 \times 3\) 的情形。
9.1. 背景#
警告
下述叙述存在主观和不可考证的内容。
卷积神经网络 (CNN) 算法一炮成名应是在 AlexNet[1] 赢得 ImageNet 2012 (ILSVRC2012) 时。在随后的几年中,CNN 算法不仅受到广泛应用与改进;其计算效率的改进也受到重视。
卷积相当于一种对图像的滤波过程,通常的加速方法是利用复空间的快速 Fourier 变换 (Fast Fourier Transformation, FFT)。卷积概念本身也与 Fourier 变换有非常直接的关联。若对物理有简单的了解,则会知道动量与坐标互为 Fourier 变换关系;而动量在自由粒子下与频率成正比,相比于坐标而言是更为全局、本征的描述子。卷积相当于某种程度上提取图像的某些全局的“频率”信息;若从这个角度来理解,卷积应当要作用于完整的一份图像。
我们可以设想,如果要通道数为 \(C_\mathrm{in}\)、大小为 \(H_\mathrm{in} \times W_\mathrm{in}\) 的图像作全局滤波,滤波所产生的输出通道数是 \(C_\mathrm{out}\);那么滤波参数就会是 \((C_\mathrm{out}, C_\mathrm{in}, H_\mathrm{in}, W_\mathrm{in})\) 大小的张量。这是会是相当夸张的张量:以 VGG16[2]为例,它处理的是通道数为 \(3\) 的 \(224 \times 224\) 图像 \(d_{cuv} \in \mathbb{R}^{3 \times 224 \times 224}\);其输出到多层感知 (MLP) 全连接层的维度是 4096,因此滤波参数的大小是 (以 32 位 float 储存)
这种全局卷积的计算量本身其实还好,甚至可能通过 FFT 加速,但参数量实在太大。同时,这种做法就是简单的线性变换,无法利用深度网络的特性——深度网络与线性变换的最大差别在于激活函数的使用。
现在常用与流行的 CNN 通常都解决了这些问题。以 VGG16 举例来说。其构造的两个最大初衷是
如果不考虑卷积层之间的激活层,那么它使用更少的参数 (500 MB 左右) 来模拟全图像的滤波过程;但代价是层数上的增加、以及计算量 FLOP 的提升 (从 1.23 GFLOP 提升到 39.02 GFLOP)。由于 GPU 显存还是比较珍贵的资源,大多数中低端显卡可用的显存大小在 3.5 GB 或以下:如果参数量就到 2.3 GB,再加上反向导数,显存就炸了。因此即使有不小的代价,但参数大小的减小对卷积问题还是很关键的。
但层数的增加不见得是坏事。如果中间引入激活层,则可以给网络带来更大的非线性;结合 VGG16 本来就不少的参数,这种非线性性质可以得到较大程度的发挥。再怎么说,大家通常更看重拟合能力;不少实际问题 (或竞赛) 对 CNN 的精度要求很高,为此牺牲一些可以接受的 FLOP 是不会心疼的。
如何对全图像的滤波过程作更少参数的拆分,大概是一门学问。它有那么些像通过张量分解以提升张量缩并运算速度。
基于这些背景,VGG16 采用了多次使用 \(3 \times 3\) 小卷积核并结合池化 (Pooling) 的策略,在其 16 层网络里,一层一层地将图像的信息全局化。由此有效地提取图像全局信息,同时减少内存压力并引入一些非线性。这也是小卷积核的由来 (不过小卷积核不是 VGG16 第一个提出的,但它应是第一个仅使用 \(3 \times 3\) 卷积核的网络)。其卷积核滤波参数大小是
但它带来的一个额外的问题是,由于卷积核太小,因此无法通过 FFT 方法加速。
在 2015-2016 年,Lavin 与 Gray 重新发现了 Winograd 在 1980 年代所提出的小型滤波的加速方法[3]。在该算法下,若只考虑实际 FLOP 数而不考虑内存通讯耗时,则可以有 2.25-9 倍的效率提升。这会是极其惊人的效率提升;不过囿于其算法的一些副作用、以及卷积问题本身所必须实现的内存通讯量,大多数实际卷积层效率提升在 1-2 倍左右,少量达到 4 倍。该算法现在通常被称为 Winograd 算法。
在这篇文档中,我们会对 Winograd 卷积过程作叙述与分析。我们会有简单的 Python 代码作说明,但由于其作为脚本语言本身的特性 (无法通过编译过程优化代码效率),Winograd 卷积无法在 Python 下展现其效率;相反地,其效率会及其严重地落后于 Direct 卷积。我们会在后一篇文档阐释 C/C++/SIMD 实现的 Winograd 卷积 (不够极限的) 提速实现。
9.2. 问题大小定义与 Direct 卷积回顾#
9.2.1. 维度大小定义#
在这篇文档中,我们通篇使用下述小型问题:
图像参数
高度 (in height)
IH\(H_\mathrm{in} = 14\);宽度 (in width)
IW\(W_\mathrm{in} = 20\);通道数 (in channel)
IC\(C_\mathrm{in} = 4\);
卷积核参数
核大小 \(K_\mathrm{H} = K_\mathrm{W} = K = 3\);
输出通道 (out channel)
OC\(C_\mathrm{out} = 16\);
分批数量 \(N = 8\)。
N = 8
IH, IW = 14, 20
IC, OC = 4, 16
OH, OW = IH - 2, IW - 2
重要的维度信息有
输入图片
image\(d_{i,c,x,y}\) 维度 \((N, C_\mathrm{in}, H_\mathrm{in}, W_\mathrm{in})\);卷积核
filtr\(g_{k,c,u,v}\) 维度 \((C_\mathrm{out}, C_\mathrm{in}, 3, 3)\)输出图片
result\(Y_{i,k,x,y}\) 维度 \((N, C_\mathrm{out}, H_\mathrm{out}, W_\mathrm{out})\)。
image = np.random.random(( N, IC, IH, IW)).astype('f') * 255
filtr = np.random.random((OC, IC, 3, 3)).astype('f')
result = np.zeros (( N, OC, OH, OW)).astype('f')
9.2.2. Direct 卷积回顾#
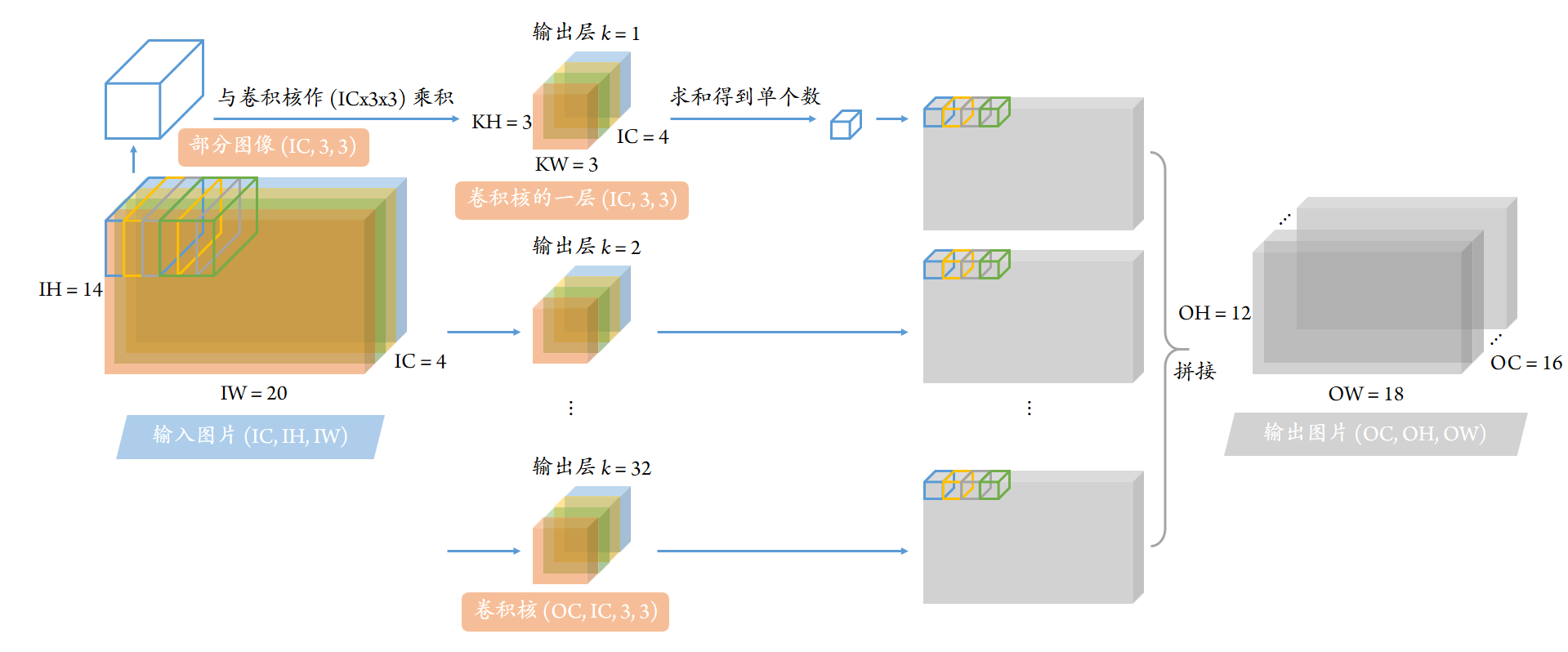
首先我们回顾到卷积计算可以写为
我们这份文档中也会利用 np.einsum 函数,因此这里同时回顾使用张量缩并方式下给出的卷积代码:
result_ref = np.empty((N, OC, OH, OW)).astype('f')
for x, y in itertools.product(range(OH), range(OW)):
result_ref[:, :, x, y] = np.einsum("kcuv, icuv -> ik", filtr, image[:, :, x:x+3, y:y+3], optimize=True)
我们也会利用矩阵记号。若将所有张量视为 \(u, v\) 的矩阵 (即下述等式右边的记号都是矩阵),则还可以写为矩阵点积:
result_ref = np.empty((N, OC, OH, OW)).astype('f')
for i, k, x, y in itertools.product(range(N), range(OC), range(OH), range(OW)):
result_ref[i, k, x, y] = (image[i, :, x:x+3, y:y+3] * filtr[k]).sum()
9.3. Winograd 算法原理实现#
这里我们完全不考虑 Winograd 算法的推导与正确性,也不考虑其效率。
Winograd 算法可以看作是将小卷积核的滤波,进行一定程度的放大,使得一次性可以输出的图像像素数增多,并减少大量浮点乘法运算。这种放大记作 \(F(M, K)\) 滤波[4]。
我们问题中的小卷积核大小始终是 \(K \times K = 3 \times 3\);
通过变换,卷积核会放大到 \(\mu \times \mu\);其中 \(\mu = M + K - 1\);
单步卷积输入图像大小也是 \(\mu \times \mu\);
单步卷积输出图像大小是 \(M \times M\)。
事实上,如果 \(M = 1\),Winograd 算法会退化到我们熟知的 Direct 卷积。
在这篇文档中,我们会以 \(M = 6\) 的情形,即 \(F(M, K) = F(6, 3)\) 作示例。在这种情况下,\(\mu = 8\) 即卷积核会滤波放大到 \(8 \times 8\) 大小。
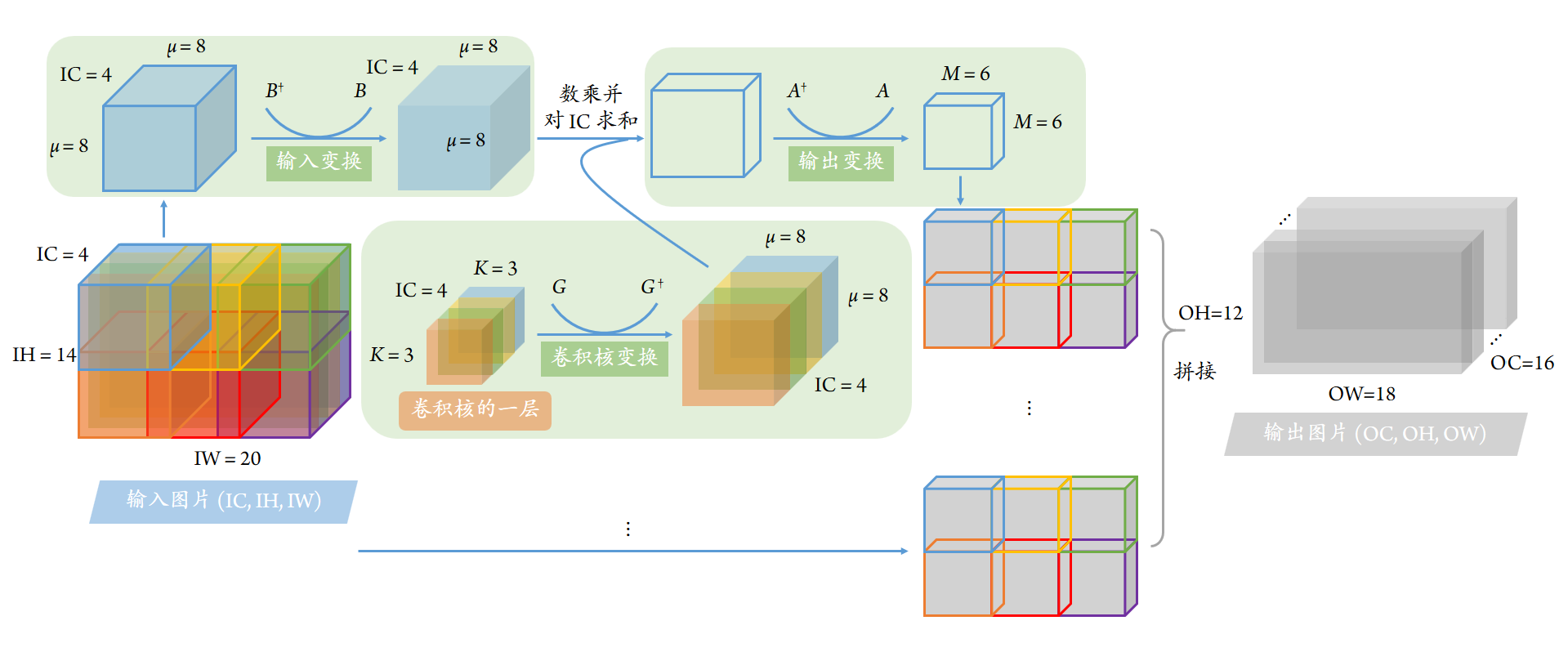
9.3.1. 输入图像变换#
不像 Direct 卷积可以一步计算到位,Winograd 算法需要四步实现。其中的第一步是输入图像变换,即图示中左上方绿色背景块中所示部分。对于输入图像
首先切割出大小为 \((N, C_\mathrm{in}, \mu, \mu)\) 的子图像 \(d^{(x,y)}_{i,c,t,w} = d_{i,c,x+t,y+w}\);
随后对其作矩阵乘法变换,得到大小为 \((N, C_\mathrm{in}, \mu, \mu)\) 的变换后的图像 \(V_{i,c,r,s}^{(x,y)}\):
\[ V_{i,c,r,s}^{(x,y)} = \sum_t^\mu \sum_s^\mu B_{t,r} d^{(x,y)}_{i,c,t,w} B_{w,s} \]如果将上式的各张量看作关于下标 \(t,w,r,s\) 的矩阵,则上式可以写作
\[ V_{i,c}^{(x,y)} = B^\dagger d^{(x,y)}_{i,c} B \]其中,\(B_{t,r} \in \mathbb{R}^{\mu \times \mu}\) 是变换矩阵,它随 \(F(M, K)\) 中 \(M, K\) 的取值不同而不同。譬如对于 \(F(6,3)\),其定义如下 (注意下述代码中使用了转置 attribute
np.ndarray.T)
B = np.array([
[ 1 , 0 , -21/4 , 0 , 21/4 , 0 , -1 , 0 ],
[ 0 , 1 , 1 , -17/4 , -17/4 , 1 , 1 , 0 ],
[ 0 , -1 , 1 , 17/4 , -17/4 , -1 , 1 , 0 ],
[ 0 , 1/2 , 1/4 , -5/2 , -5/4 , 2 , 1 , 0 ],
[ 0 , -1/2 , 1/4 , 5/2 , -5/4 , -2 , 1 , 0 ],
[ 0 , 2 , 4 , -5/2 , -5 , 1/2 , 1 , 0 ],
[ 0 , -2 , 4 , 5/2 , -5 , -1/2 , 1 , 0 ],
[ 0 , -1 , 0 , 21/4 , 0 , -21/4 , 0 , 1 ],
]).T.astype('f')
现在我们将变换后的图像写出。但需要注意的是,与 Direct 情形不同,我们不需要对每个 \(x = 0, 1, \cdots, H_\mathrm{in} - 2\) 作卷积计算;而是对 \(x = 0, M, 2M, \cdots\) 即 \(x = 0, 6, 12 \cdots\) 作计算。我们会用 \(\tilde x = x / M\) 作替代。对于 \(\tilde y = y / M\) 也作相同处理。
高方向上需作的卷积处理次数
TH\(\tilde H = H_\mathrm{out} / M = 2\);宽方向上需作的卷积处理次数
TW\(\tilde W = W_\mathrm{out} / M = 3\);
TH, TW = OH // 6, OW // 6
那么变换后的图像 V \(V_{i,c,r,s}^{(\tilde x, \tilde y)}\) 则可以写作维度为 \((\tilde H, \tilde W, N, C_\mathrm{in}, \mu, \mu)\) 大小的张量 (对应角标是 \(\tilde x, \tilde y, i, c, r, s\))。我们首先按下式来计算:
V = np.empty((TH, TW, N, IC, 8, 8)).astype('f')
for x_, y_, i, c in itertools.product(range(TH), range(TW), range(N), range(IC)):
x, y = 6 * x_, 6 * y_
V[x_, y_, i, c] = B.T @ image[i, c, x:x+8, y:y+8] @ B
如果用 np.einsum 作张量缩并,则也可以写为
V = np.empty((TH, TW, N, IC, 8, 8)).astype('f')
for x_, y_ in itertools.product(range(TH), range(TW)):
x, y = 6 * x_, 6 * y_
V[x_, y_] = np.einsum("tr, ictw, ws -> icrs", B, image[:, :, x:x+8, y:y+8], B, optimize=True)
9.3.2. 卷积核变换#
维度为 \((C_\mathrm{out}, C_\mathrm{in}, K, K)\) 的卷积核 \(g_{k,c,u,v}\) (相当于 \(K \times K\),在我们的问题下是 \(3 \times 3\) 的卷积核) 在 Winograd 算法下,需要滤波增大到 \((C_\mathrm{out}, C_\mathrm{in}, \mu, \mu)\) 维度 (相当于 \(\mu \times \mu\),在我们的问题下是 \(8 \times 8\) 的放大滤波)。其计算过程如下:
与刚才一样,变换矩阵 \(G_{r,u} \in \mathbb{R}^{\mu \times K}\) 随着 \(F(M, K)\) 中 \(M, K\) 取值不同而不同。对于我们的问题而言,\(K = 3\), \(\mu = 8\);因此卷积核相当于被放大了 7.1 倍。
G = np.array([
[ 1 , 0 , 0 ],
[ -2/9 , -2/9 , -2/9 ],
[ -2/9 , 2/9 , -2/9 ],
[ 1/90 , 1/45 , 2/45 ],
[ 1/90 , -1/45 , 2/45 ],
[ 32/45 , 16/45 , 8/45 ],
[ 32/45 , -16/45 , 8/45 ],
[ 0 , 0 , 1 ],
]).astype('f')
U = np.einsum("ru, kcuv, sv -> kcrs", G, filtr, G, optimize=True)
我们也可以用矩阵乘法来给出该过程 (即将各张量看作关于 \(u, v, r, s\) 的矩阵):
U = np.empty((OC, IC, 8, 8)).astype('f')
for k, c in itertools.product(range(OC), range(IC)):
U[k, c] = G @ filtr[k, c] @ G.T
9.3.3. 数乘#
第三步是将变换后的图像与卷积核作数乘,并对输入通道作求和缩并:
这一步比较适合用 np.einsum 来解决:
M = np.einsum("kcrs, xyicrs -> xyikrs", U, V, optimize=True)
这一步也会写成如下的矩阵形式:
M = np.zeros((TH, TW, N, OC, 8, 8)).astype('f')
for x_, y_, i, k, c in itertools.product(range(TH), range(TW), range(N), range(OC), range(IC)):
M[x_, y_, i, k] += U[k, c] * V[x_, y_, i, c]
9.3.4. 输出图像变换#
最后一步是进行输出图像变换:
我们注意到,输出图像应当是 \((N, C_\mathrm{out}, H_\mathrm{out}, W_\mathrm{out})\) 的四维张量 \(Y_{i,k,x,y}\),而不适合写成六维张量 \(Y_{i,k,a,b}^{(\tilde x, \tilde y)}\) 的形式。这一步用到的变换矩阵是 \(A_{r,a} \in \mathbb{R}^{\mu \times M}\)。
A = np.array([
[ 1 , 1 , 1 , 1 , 1 , 1 , 1 , 0 ],
[ 0 , 1 , -1 , 2 , -2 , 1/2 , -1/2 , 0 ],
[ 0 , 1 , 1 , 4 , 4 , 1/4 , 1/4 , 0 ],
[ 0 , 1 , -1 , 8 , -8 , 1/8 , -1/8 , 0 ],
[ 0 , 1 , 1 , 16 , 16 , 1/16 , 1/16 , 0 ],
[ 0 , 1 , -1 , 32 , -32 , 1/32 , -1/32 , 1 ],
]).T.astype('f')
result = np.empty((N, OC, OH, OW)).astype('f')
for x_, y_ in itertools.product(range(TH), range(TW)):
x, y = 6 * x_, 6 * y_
result[:, :, x:x+6, y:y+6] = np.einsum("ra, ikrs, sb -> ikab", A, M[x_, y_], A, optimize=True)
np.allclose(result, result_ref)
True
如果写为关于下标 \(a, b, r, s\) 的矩阵乘法,则
result = np.empty((N, OC, OH, OW)).astype('f')
for x_, y_, i, k in itertools.product(range(TH), range(TW), range(N), range(OC)):
x, y = 6 * x_, 6 * y_
result[i, k, x:x+6, y:y+6] = A.T @ M[x_, y_, i, k] @ A
np.allclose(result, result_ref)
True
至此,我们就给出了 Winograd 算法的实现过程。
9.3.5. 总表达式#
在 Lavin 2016 原始文献的公式 (8),给出了以矩阵乘法为表示的总表达式。以这篇文档的记号重述为
因此,尽管 Winograd 算法比起 Direct 算法还是要复杂不少,但若提前对 \(A, B, G\) 变换矩阵有所定义,且不考虑效率,那么核心的代码其实也就 2-3 行。
result = np.zeros((N, OC, OH, OW)).astype('f')
for x_, y_, i, k, c in itertools.product(range(TH), range(TW), range(N), range(OC), range(IC)):
x, y = 6 * x_, 6 * y_
result[i, k, x:x+6, y:y+6] += A.T @ ((G @ filtr[k, c] @ G.T) * (B.T @ image[i, c, x:x+8, y:y+8] @ B)) @ A
np.allclose(result, result_ref)
True
9.4. Winograd 算法讨论#
在这一部分中,我们会简单讨论 FLOP 数问题。
我们首先回顾到,对于 Direct 算法而言:
或者用更为适合分析 FLOP 的公式:
其 FLOP 在前一篇文档中已经有所分析:
对于我们当前的问题,\(C_\mathrm{out} = 16\), \(C_\mathrm{in} = 4\), \(H_\mathrm{out} = 18\), \(W_\mathrm{out} = 12\);因此,
9.4.1. 变换过程 FLOP:以输入图像为例#
我们首先回顾变换过程的计算表达式:
它是两步矩阵乘法所构成的,且每一步矩阵乘法的 FLOP 数一致。其中一步矩阵乘法是
这一步的 FLOP 计算可以通过将所有角标对应的维度相乘 (\(\tilde x, \tilde y, c, t, r, w\),但除去分批数量角标 \(i\)),并考虑到加法与乘法而要额外乘以 2:
考虑到两步矩阵乘法过程,因此输入图像转换就需要经过约 50k 的 FLOP 运算。它已经是 Direct 卷积总计算量的 20%,已是个不小的数值了。
但实际上,我们并不真的需要真的进行矩阵乘法。我们现在考虑图像变换问题的子问题,即矩阵乘法 \(T = B^\dagger D\) (其中 \(B, D \in \mathbb{R}^{\mu \times \mu}\)):
如果要依照矩阵乘法的算法进行计算,则其 FLOP 数是 \(2 \mu^3 = 2 \times 8^3 = 1024\),或者是 128 次长度为 \(\mu = 8\) 的向量运算。但有意思的是,如果我们细致地分析矩阵 \(B\):
就能发现该矩阵实际上是有特征的。
首先考虑到 \(T_0 = (B^\dagger D)_0 = D_0 - 5.25 \times (D_2 - D_4) - D_6\) (我们采用零索引 0-index),它的计算量是 3 次向量加法与 1 次向量乘法;每个向量长度是 \(\mu = 8\),因此这一步的 FLOP 是 32。对于 \(T_7\) 也有同样的结论。
随后对于 \(T_1, T_2\) 而言,
\[\begin{split} \begin{align*} T_1 &= (D_2 - 4.25 \times D_4 + D_6) + (D_1 - 4.25 \times D_3 + D_5) \\ T_2 &= (D_2 - 4.25 \times D_4 + D_6) - (D_1 - 4.25 \times D_3 + D_5) \end{align*} \end{split}\]我们注意到如果可以预留两个寄存器,分别储存
\[\begin{split} \begin{align*} s_0 &= D_2 - 4.25 \times D_4 + D_6 \\ s_1 &= D_1 - 4.25 \times D_3 + D_5 \end{align*} \end{split}\]那么作为结果的向量则是 \(T_1 = s_0 + s_1\), \(T_2 = s_0 - s_1\)。生成 \(s_0, s_1\) 时需要 4 次向量加法与 2 次向量乘法;生成 \(T_1, T_2\) 需要 2 次额外的向量加法。每个向量长度是 \(\mu = 8\),因此这一步的 FLOP 是 64。
对于 \(T_3, T_4, T_5, T_6\) 而言,其计算方式与 \(T_1, T_2\) 类似;但由于浮点数值不太相同,因此额外需要引入 3 次向量乘法,因此生成 \(T_3, T_4\) 和 \(T_5, T_6\) 分别需要的 FLOP 数是 88。
因此总地来说,\(T = B^\dagger D\) 需要的 FLOP 数是 \(32 + 64 + 88 + 88 + 32 = 304\),或者 38 次长度为 \(\mu = 8\) 的向量运算。这要明显比普通的矩阵乘法的 1024 次要少很多。除此之外,如果我们允许 FMA (Fused Multiply Addition/Accumulate) 与 SIMD (Single Instruction Multiple Data),那么实际运算数可以再少一些。
我们不妨考察下述 C++ 代码:
// input.cpp
#include <immintrin.h>
#define Intrinsic __m256
void transform_BtD_6x3(const Intrinsic D[8], Intrinsic BtD[8]) {
Intrinsic s0, s1;
BtD[0] = D[0] + 5.25f * (D[4] - D[2]) - D[6];
BtD[7] = D[7] - D[1] + 5.25f * (D[3] - D[5]);
s0 = D[1] - 4.25f * D[3] + D[5];
s1 = D[2] - 4.25f * D[4] + D[6];
BtD[1] = s0 + s1;
BtD[2] = s1 - s0;
s0 = 0.5f * D[1] - 2.5f * D[3] + 2.f * D[5];
s1 = 0.25f * D[2] - 1.25f * D[4] + D[6];
BtD[3] = s0 + s1;
BtD[4] = s1 - s0;
s0 = D[1] + D[1] - 2.5f * D[3] + 0.5f * D[5];
s1 = 4.f * D[2] - 5.f * D[4] + D[6];
BtD[5] = s0 + s1;
BtD[6] = s1 - s0;
}
我们通过 gcc 生成汇编代码:
$ g++ input.cpp -S -march=native -O3
可以寻找到汇编代码中,如果不考虑向量移动指令 vmovaps (尽管向量移动经常才是耗时步,但不要在意太多细节 >.<)
vsubps,vaddps出现 15 次,用于向量加法与减法;vfmadd___ps出现 10 次,用于向量乘法累加;vmulps出现 3 次,用于向量乘法;
因此,允许 FMA 与 SIMD 下,\(T = B^\dagger D\) 的实际浮点运算数是 28 次向量运算,且每次向量运算消耗的浮点运算数是 1 而非 \(\mu = 8\)。除此之外,在第二、三次生成 s1 中,如果利用加法交换律,是可以进一步减少两次向量乘法而变为向量乘法累加的,因此可以减少到 26 次向量运算。这比起普通的乘法需要 \(2 \mu^2 = 128\) 次向量运算要少许多运算量 (大约只有 20%)。不仅如此,普通乘法的汇编实现还需要较多的 boardcast, shuffle 等比较耗时的操作;但依据 \(B\) 矩阵的特征而作的实现则基本不需要这些。
因此,总地来说,利用 \(B\) 矩阵的特征作输入图像变换,可以提速到 20% 甚至更快。在这种情形下,计算耗时仅有 Direct 卷积耗时的 4%。因此,如果图像或卷积核变换实现地高效,那么这些变换相对于总计算耗时来说,会次要一些。
这里只是定性的叙述。我们会在下一篇文档中,关于图像与卷积核变换的效率提升作更为详细的描述。
9.4.2. 数乘 FLOP:最耗时步#
我们回顾到数乘步骤是
其 FLOP 数仍然是将所有角标对应的维度相乘 (\(\tilde x, \tilde y, k, c, r, s\),但除去分批数量角标 \(i\)) 并乘以 2:
这大约是 Direct 卷积 FLOP 数的 20%。从这里就能看出 Winograd 算法相对于 Direct 算法的效率提升的主要来源了。综合图像与卷积核变换的消耗,Winograd \(F(6,3)\) 的 FLOP 数可以达到 Direct 算法的 30%-40% 左右;这是非常惊人的提升了。
我们可以在此回顾 Winograd 算法与 Direct 算法两者的图像表示。我们看到输入图像中,对于 Direct 算法而言,图像上的大多数像素都被遍历了 9 次;但 Winograd \(F(6,3)\) 算法中,其中不少像素只被遍历了 1 次;只有少量的像素被遍历 2 或 4 次。这就是 Winograd 算法通过放大滤波而减少数乘计算量,从而减少总计算量的直观解释。
但为了放大滤波大小 \(\mu\),Winograd 算法要求事先与事后要对图像和卷积核作变换;这是代价。由于变换的成本随着滤波大小 \(\mu\) 呈平方级增长,但数乘最多只能降低 9 倍 (每个像素必然要被遍历一遍),因此滤波大小不可能无限地放大。一般程序的实现中,滤波大小 \(\mu\) 通常取到 4 或 6。我们在这份工作中使用的滤波大小是 \(\mu = 8\)。在下一篇文档中,我们会指出,显然 \(\mu = 8\) 没有达到理论最大加速;但若考虑到计算机缓存大小的因素,\(\mu = 8\) 应当基本到极限了。
读者不妨通过展开下述两个折叠块,重新直观地检视与比对 Direct 算法与 Winograd 算法。
Direct 卷积算法图示
Winograd 卷积算法图示

